摘要:文章结合e-b梁模型得到了列车荷载作用下地基的振动响应方程,结合该方程对上海地铁一号线现场实测的列车振动进行模拟,计算的位移幅值与实测值比较吻合,曲线形状也基本一致,表明计算模型能够反映出列车引起的轨道结构振动。
关键词:列车 振动 e-b梁 轨道
一个半世纪以来,铁路运输这一重要的运输方式得到了长足的发展。尤其是铁路高速客运列车的问世,使铁路运输成为航空和高速公路等交通手段的强有力竞争者。高速铁路运输环境污染少,成本低,速度快,运行准点、安全等优点,在很多国家得到了重视和发展。但是在列车速度提高的同时,也出现了严重的环境振动和噪声污染问题。高速列车会在轨道和地基中产生很大的振动,尤其当列车的运行速度接近轨道地基系统的临界速度时,能量不能在轨道结构和周围地基中及时逸散,从而产生过大的振动。除此之外,随着高速铁路线的广泛延伸,铁路线不可避免的会穿越或临近对振动敏感的居民区或工业区,影响居民的正常生活,造成精密仪器的非正常工作。因此研究列车引起的轨道和地基振动,对列车的安全性评估,铁路的合理、经济设计具有重要的工程应用价值。
1 列车荷载引起振动的分析方法
列车产生的振动通过轨道结构(包括钢轨、枕木、道碴、下垫层)向外扩散,在地基中以应力波的形式传播,之后被铁路沿线或隧道上部的居民所感受到。振动从列车传播到周围结构中的过程可以分成三个阶段:1)振动的产生;2)传播、衰减;3)接收。每个阶段都有很多因素可以影响最终的振动水平,主要的因素包括列车类型,列车车速,路堤的设计,地基条件,结构物的地基,结构物类型和结构物距铁路线的距离。由于缺乏对这些因素的深入研究,分析列车振动就变得十分困难。然而,在某些情况下,利用试验和理论结果还是可以对振动进行合理的预测。首先要确立合理的荷载模型来模拟列车作用于轨道上的荷载。对列车产生的地基振动,荷载可以简化为随时间变化的力或移动点荷载。荷载模型确定后,就可以通过轨道结构模型预测分析路堤的响应。接下来就要分析振动的传播和地基响应,这个模型可以是独立的,也可以与轨道结构模型耦合。当分析地基与结构物基础的相互作用时,必须考虑振动的传播;而分析结构物的响应时,可以只考虑传递到结构物上的运动。
2 e-b梁模型
winkler地基—e-b梁模型是分析地基振动的最简单模型。前者将地基简化为相互独立的弹簧,且弹簧常数不变;后者忽略了剪切变形,只考虑弯曲变形。这种模型可大大降低问题的复杂度,因此被广泛采用。
2.1 控制方程
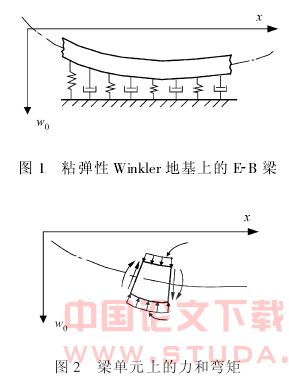
图1,图2是粘弹性winkler地基上梁的模型,假设弹簧刚度和阻尼器的阻尼都是连续的,产生线性的反力
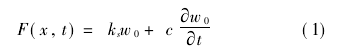
式中,f(x,t)为地基作用于梁单位长度上的反力,ks为弹簧常数,c为粘性系数。
由单元竖向力平衡并利用公式(1)可得
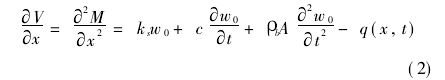
式中,ρb为梁的质量密度,a为梁的横截面积,q(x,t)为作用于梁单位长度上的外荷载。
梁的变形符合平截面假定,所以有
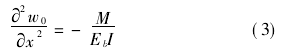
式中,ebi为梁的抗弯刚度,eb为梁的杨氏模量,i为梁的截面惯性矩。
代入公式(2)可得粘弹性winkler地基上e-b梁的控制方程
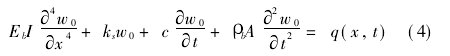
2.2 动力解答
动力问题包括惯性力,在移动集中荷载作用下的弹性地基(无阻尼)梁的控制方程为
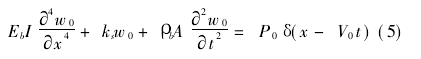
引入移动坐标后,控制方程化为

根据叠加原理,列车荷载引起的总位移为

3 模型计算结果与实测值比较
采用e-b梁在列车荷载作用下的模型以及对应的公式对上海地铁一号线现场实测的列车振动进行模拟。
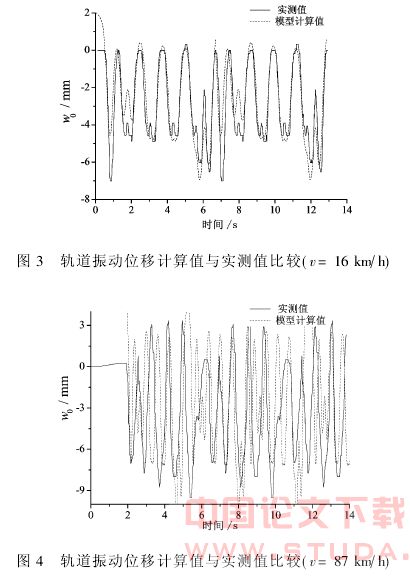
图3、图4是列车车速分别为16km/h、87km/h的轨道振动位移计算值与实测值的对比。从中可以看出,计算的位移幅值与实测值比较吻合,曲线形状也基本一致,表明计算模型能够反映出列车振动的主要机理———轨道结构振动。
4 结论
本文结合e-b梁模型得到了列车荷载作用下地基的振动响应方程,结合该方程对上海地铁一号线现场实测的列车振动进行模拟,计算的位移幅值与实测值比较吻合,曲线形状也基本一致,表明计算模型能够反映出列车的轨道结构振动。
参考文献
[1]kenneyjt.steady-statevibrationsofbeamonelasticfoundationformovingload[j].journalofappl.mech,1954,(76):359-364.

