摘 要: 概述了地铁列车运行仿真计算涉及的数学模型, 提出用问题分解法求解地铁列车在线路上运行仿真过程, 并给出了通过限速和停站的高效算法。

关键词: 地铁列车; 运行; 仿真计算; 数学模型; 问题分解; 算法
 
1 概述
      地铁列车运行仿真的主要任务是根据不同载荷、不同线路、不同供电、不同动车损失、不同运行策略等条件,研究地铁车辆运行的基本算法、关键参数的取值对牵引运行的影响以及不同运行策略时的计算模型, 计算列车在运行过程中速度、距离、电流、能耗和时间的关系( v=v( t) , s=s( t) , i=i( t) , w=w( t)) , 并绘制相应的特性曲线, 为地铁线路设计、列车设计、列车运用提供理论依据。
2 计算输入
      实现列车运行仿真计算, 需输入以下基本数据:
      1) 列车负载数据: 动车 / 拖车 / 空车质量、运行载荷、旋转系数;
      2) 线路端面数据: 各站距离和停站时间、坡度、曲线、限速、电网电压;
      3) 牵引和制动特性 f( v) ;
      4) 基本阻力和附加阻力公式 r( v) ;
      5) 电流、能耗特性 (i v) 、w( v) , 或数据表格, 该特性或数据由电机制造商提供。
      在进行列车运行仿真计算时, 要进行仿真计算设置, 即选择列车和线路、时间步长值( 0.1～0.01 s) 、施加的负载、牵引及电制动的失效率。不同的计算设置会产生不同的仿真结果, 通过分析计算结果可以得到关键参数的取值对列车运行的影响。
3 计算模型
      地铁列车在运行过程中速度随时间不断变化, 即 v =v( t) , 因此, 列车的牵引力 f=f( v) 和运行阻力 r=r( v) 也会不断变化。为方便分析和计算, 把列车看作一个质点,并假设 v= v( t) 是连续的, 即△t→0; △v→0。
3.1 计算阻力
      列车运行阻力由基本阻力和附加阻力组成, 即 r( v)=r基( v) +r附( v) , r基采用东洋电机公司的 jis 公式:
      r 基 =( 1.65+0.0247v) ×mm+( 0.78+0.0028v) ×mt+( 0.028+0.0078( n- 1)) v2
      式中: mm—动车总质量; mt—拖车总质量; n—车厢数量;v—列车速度。
      附加阻力 r 附包括曲线阻力和坡道阻力。
r 附 =( 600/r+gd) ×m
      式中: r—线路曲线半径; gd—线路坡度; m—列车总质量。
3.2 计算加速度
      根据 f=ma, 可计算出列车的加速度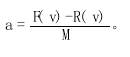
 
3.3 计算速度
      由于时间步长设置较小, 即△t= ti+1- ti 变化不大, 在△t的时间间隔内的平均加速度可用初始加速度 ai 代替, 则列车的运行速度 vi+1 为:
vi+1=vi+ai×△t
      式中: vi+1 为第 ( i+1) 步的速度; vi 为第 i 步的速度; i=0,1, 2, …。
3.4 计算距离
      对速度进行积分, 由于△t= ti+1- ti 变化不大, 在△t 的时间间隔内的速度可用其平均速度, 则列车的运行距离si+1=si+0.5×( vi+vi+1) ×△t。
3.5 计算电流
      根据输入的电流特性数值表 (i v) 和速度 vi, 通过查表取得 i0 (v0) 和 i k (vk) , 其中 v0≤vi<vk , 通过线性插值求出 vi对应的电流 ii, 就可以得到电流和时间的关系 i=(i t) 。
4 仿真算法
4.1 仿真过程分解
      列车在整个线路的运行仿真计算过程是按时间步长( 如 0.05 s) 循环进行的, 整个计算过程可以分解对两站之间的运行计算子过程, 站间仿真子过程进一步分解为成区间计算子过程。如果两站间有 n 个限速区, 站间计算子过程就分解成( n+1) 区间仿真计算过程, 整个计算过程就简化成由( n+1) 个区间计算过程组成。

4.2 区间计算过程
      向量 x( v, a, s, t) 表示列车的运行状态, 向量空间 x 是x 的集合( x={x}) , 也就是仿真计算结果, 时间步长算法可以抽象成空间 x 上的一个映射, 算法的每一步都是 xi转变成 xi+1 。计算过程就是从确定 x0 开始经过不断映射( x0→x1→x2…→xn) 的循环过程。
      为了提高区间计算过程的速度, 如图 1 所示, 把计算过程分解成正反两个阶段, 避免在每个步长计算中, 进行限速或停站制动试凑。

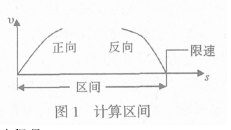
      区间计算过程是:
      1) 计算反向阶段得到数据集 x 反;
      2) 计算正向阶段得到数据集 x 正;
      3) 根据 x 正中的最后一个量 xn , 除去 x 反 中速度大于xn 的速度的量集 xs;
      4) 计算结果 x=x 正 +{ x 反 - xs}。
4.2.1 反向计算
      从限速区( 停站可以认为限速为 0) 开始位置反向计算, 即把制动力和阻力取反, 算法如下:
      1) 如果 vi <vh×δ惰行, 牵引力 f 从制动特性获取;
      2) 计算阻力 r, 加速度 ai , 速度 vi+1 , 距离 si+1;
      3) 设置 ti+1=ti+△t, 把 xi+1 存入 x 反;
      4) 如果 vi+1≥vh×δ则结束, 否则转步骤 1) 。
4.2.2 正向计算
      从起始位置( 或限速区结束位置) 开始正向计算, 算法如下:
      1) 如果 vi<vh×δ加速, 牵引力 f 从牵引特性获取, 转步骤 5) ;
      2) 如果 vi≤vh×δ惰行, 牵引力 f=0, 转步骤 5) ;
      3) 如果 vi≥vh 减速, 制动力 f 从制动特性获取, 转步骤 5) ;
      4) 计算阻力 r, 加速度 a i, 速度 vi+1, 距离 si+1 ;
      5) 设置 ti+1=ti+△t, 把 xi+1 存入 x 正;
      6) 检查是否进入反向区, 是则转步骤 8) , 否则转步骤i) ;
      7) 根据 vi+1获得 xs , 合并 x 正 和 {x 反 - xs}, 把 vh 置为v 限;
      8) 如果 si+1 接近限速区的结束位置则结束, 否则转步骤 2) 。
      以上, vh 为列车最高速度, v 限 为限速区的限速, δ是与时间步长有关的量, 取值在 0.965 到 0.995 之间。
5 结束语
      地铁列车牵引仿真算法设计对地铁列车牵引仿真软件设计有重要的指导意义, 建立一套完善仿真软件系统,有助于地铁线路和列车的技术设计和方案论证。本文旨在起到一个抛砖引玉的作用, 欢迎同行赐教。
 
参考文献:
[1] 刘 云. 列车运行仿真系统的软件设计[j] . 北方交通大学学报,1995( 3) .
[2] 张中央. 列车牵引计算[m]. 北京:中国铁道出版社, 2000.
[3] 毛保华. 通用列车运行模拟软件系统研究[j]. 铁道学报, 2000( 1) .
[4] 程 曙, 林伟侵. 地铁牵引仿真研究[j]. 城市轨道交通研究, 2002( 5) .