摘要:机场轨道交通的发展将是解决机场陆侧交通拥堵问题的主要途径之一.本文首先通过灰色预测模型gm(1,1)对首都机场的陆侧交通量进行预测,得出进出机场的旅客中乘坐机场巴士及出租车的人数.在此基础上,运用排队论的方法,分析机场轨道交通对机场巴士及出租车交通量的分流情况,得出各自具体的分流率和分流量.最后,根据马尔可夫链的方法,对分流情况的发展趋势进行分析,得出其稳定分流率.
关 键 词:灰色预测;排队论;马尔可夫链;机场轨道交通;分流率
1前言
随着航空业务需求量的不断增长,进出机场的旅客日益增多,不可避免地会给机场陆侧交通带来更大的压力.据统计,2004年首都机场旅客吞吐量已达到3488万,并且继续保持着较快的发展势头.根据首都机场消费者调查及ibm行业分析,目前进出首都机场的地面交通方式主要有出租车,巴士和自备车,其中乘坐出租车和自备车的旅客高达80%,而承载量相对较大的机场巴士却只占很小的比例,进出机场的道路交通已经产生明显的瓶颈.
为了缓解首都机场陆侧交通的压力,需要考虑一个大容量的轨道交通体系.北京市规划委员会于2005年3月4日审批通过了《东直门至机场快速轨道规划方案》.机场轨道线全线27.76公里,拟设4座车站,即东直门站、麦子店西站、t2及t3航站楼站.列车时速拟为100公里左右,从东直门出发,15至17分钟可到达首都机场.
机场轨道交通作为大容量的公共服务设施,与巴士及出租车共同承担着进出机场的旅客运输.但是,机场轨道交通的建成通车对机场巴士及出租车将产生怎样的定量影响,对陆侧交通压力的缓解将产生多大的作用,已经成为人们密切关注并需要深入研究的问题.
2 基于gm(1,1)模型对首都机场陆侧交通量进行灰色预测
2.1 gm(1,1)模型的原理
灰色预测采用将原始数据进行直接累加、移动平均加权累加等方式,使生成数列呈现一定的规律性,利用典型曲线逼近其相应曲线,以逼近的曲线作为模型,对系统进行预测.在gm(1,1)中,以-作为系统发展系数,以作为灰色作用量,则可以得到预测模型为[1]:
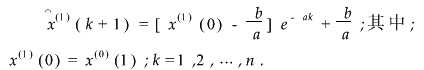
为了使gm(1,1)模型能够达到预测的精度要求,需要对其进行残差检验及后验差检验[2].如果能够满足表1所示的模型精度等级要求,则可以采用所建模型进行预测,否则需要对模型进行残差修正.
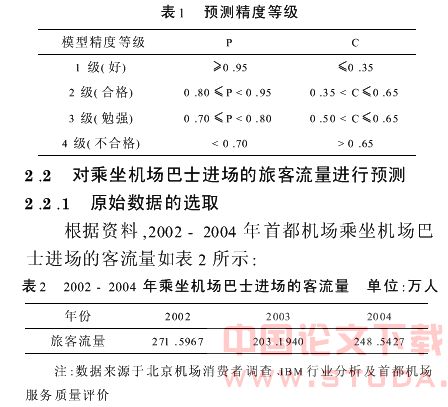

由c=0.01<0.35,p=1.00>0.95,根据表1预测精度等级可以得出结论,该模型精度等级为1级,有较好的预测精度和实用价值.
2.2.4 预测结果
根据式(1)预测模型,对首都机场2005-2008年乘坐机场巴士进场的旅客流量进行预测,预测结果见表5所列.
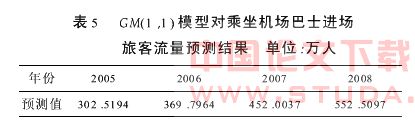
同理,我们对首都机场2005-2008年乘坐出租车进场的旅客流量进行预测,预测结果见表6所列.

3用排队论方法分析机场轨道交通的分流率
由于机场轨道交通对进出场的旅客将会产生较大的吸引力,尤其是对乘坐机场巴士和出租车的旅客,其影响力是很大的.我们将运用排队论的方法来研究机场轨道交通对机场巴士及出租车交通量具体的分流情况.
3.1轨道交通与机场巴士
3.1.1多通道损失制排队系统原理
在/m/m/s/m排队系统中,当时,我们称该系统为多通道损失制排队系统,即当s个服务台均不空时,顾客来到服务系统不予服务,顾客立即离去,另求服务.顾客因系统饱和而未进入系统的概率称为系统损失率[3],即:

其中,ρ为服务强度,指相同时间间隔内顾客的平均到达数与能被服务的平均数之比.
3.1.2 运用多通道损失系统分析轨道交通对机场巴士的分流率
在首都机场,承担进场旅客运输的巴士总共有5条线路,设有5个站点,分别为雅宝路站、西单站、公主坟站、方庄站及中关村站.当旅客到达量超过机场巴士运送能力时就会出现旅客排队的现象.如果将机场巴士看作“顾客”,将巴士运营看成“服务机构”,机场巴士与巴士的运营就构成了5通道排队系统m/m/5.
机场轨道交通通车后,由于其具有的吸引作用,必然有相当一部分改乘轨道交通.此时,机场巴士及运营就构成了多通道损失系统.在每条线路上,平均每隔15分钟有一辆车进站,则原来在站上等待的车就准备出发,所以巴士最多可以有5个位置来排队等候,即系统容量为5,多通道损失系统为m/m/5/5.
根据上述预测,到2008年,乘坐机场巴士进场的旅客将达到552.5097万人,则每小时将达到1262人.按照巴士有效座位数34人/车计算,则要求每小时保证38辆巴士进行运营.根据其平均每间隔15分钟出发一次的标准来计算,每条线每小时出发4辆.即有:
m=s=5;λ=38辆/小时;u=4辆/小时;ρ=1.90
据此,根据式(2)可以计算出机场巴士的损失率为:pm=54.81%
这损失可以认为是全部流向机场轨道交通的,而巴士的保留率为1-pm=45.19%,进而可以计算出乘坐轨道交通及巴士进场的旅客量转移情况.见表7所示.

3.2轨道交通与出租车
我们同样采用排队论的方法来分析轨道交通对出租车的分流率.但由于出租车与机场楼前道路通行能力构成单通道损失制排队系统m/m/c/c,其中c=1,则系统损失率为[4]:
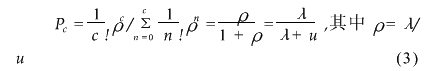
根据上述预测,到2008年,乘坐出租车进场的旅客将达到1224.3077万人,则每小时将达到2795人.按照出租车有效座位数1.1人/车计算,则要求每小时保证2541辆出租车进行运营.根据《城市道路设计规范》,首都机场的进出场道路通行能力均为3280辆/小时,由比例分析可知出租车通行能力为1310辆/小时.即有:
λ=2541辆/小时;u=1310辆/小时;ρ=1.94
据此,根据式(3)可以计算出出租车的损失率为:pc=65.98%
这损失可以认为是全部流向机场轨道交通的,而出租车的保留率为1-pm=34.02%,进而可以计算出2008年首都机场乘坐轨道交通及出租车的旅客量转移情况.见表8所示.

4 用马尔可夫链法对机场轨道交通的稳定分流率进行预测
由上述分析可知,当首都机场轨道交通建成通车后,对其陆侧交通将会产生重大的影响.然而,对于这种影响的发展趋势及其将来的结果,我们采用马尔可夫链的方法进行分析.
4.1马尔可夫链法的基本原理
马尔可夫链法常用来研究事物的状态转移情况,即从事物初始所处的状态出发,去分析经过若干时间间隔后,事物将转变成何种状态.我们采用马尔可夫链法来分析轨道交通对机场巴士及出租车分流率的发展趋势,以及最终达到平衡状态时的分流率,即稳定分流率.
我们令p为一步转移概率矩阵,并且对所有i和j满足:σjpij=1及pij >= 0.由于初始状态对n步转移概率的影响随n的增大而越来越小.因此,当n趋于时,可以从n步转移概率直接取得稳态的概率分布,并不需要考虑其初始状态.令πj为稳态概率分布的集合,则可得稳态方程组为[5]:
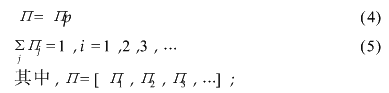
4.2轨道交通对机场巴士的稳定分流率
根据上述分析的轨道交通对机场巴士在2008年的分流率及分流量,可得到如下数据:
1)机场巴士与轨道交通分别对机场进场旅客的吸引系数

由此可得,轨道交通对进场旅客的吸引平均年增长率为:0.1256×0.4954=0.0622,则从机场巴士转向轨道交通的转移概率为0.0622;机场巴士对进场旅客的吸引平均年增长率为:0.1256×0.0731=0.0093,则从轨道交通转向机场巴士的转移概率为0.0093.
3)根据需要满足的条件可得,轨道交通自身的转移概率为1-0.0093=0.9907;机场巴士自身的转移概率为1-0.0622=0.9378.则可以得出转移概率矩阵p为:
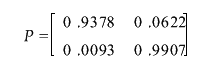
4)根据式(4)、式(5)计算可知,当达到平衡状态时,机场巴士的稳定分流率为13.01%,轨道交通的稳定分流率为86.99%.
4.3 轨道交通对出租车的稳定分流率
同理,采用马尔可夫链法分析出租车与轨道交通的稳定分流率,根据式(4)、式(5)计算可知,当达到平衡状态时,出租车的稳定分流率为18.52%,轨道交通的稳定分流率为81.48%.
5 结论
目前,机场巴士与出租车的运输能力合计为2121人/小时,而机场轨道交通的运输能力将达到9600人/小时,是前两者运输能力的4倍多.同时,机场轨道交通具有速度快、准点率高、价格合理等优点,所以对进场旅客的吸引力是相当大的.由分析可知,轨道交通开通运营后,将吸引机场巴士约54. 81%、出租车约65.98%的进场旅客.随着城市其他轨道交通的建立与完善,机场轨道交通的换乘将更为方便,其作用将得到进一步的发挥.
根据上述预测结果可知,如果不考虑机场轨道交通的情况,到2008年,机场巴士的运量约为552.5097万人/年,出租车的运量约为1224.3077万人/年,两者合计约为1776.8174万人/年,将会给机场陆侧交通带来严重的压力.根据机场轨道交通的设计参数,其运输能力可以达到4204.8000万人/年.可见,只要轨道交通能充分发挥其作用,有效地承担起进出场旅客的运输,将会大大缓解机场陆侧交通的压力.
因此,在机场轨道交通建成通车后,其对机场巴士的分流率由起初的54.81%呈递增趋势,最后稳定在86.99%;对出租车的分流率由起初的65.98%呈递增趋势,最后稳定在81.48%.这充分体现了机场轨道交通在首都机场陆侧交通中所起的积极作用,也充分肯定了在首都机场建设机场轨道交通的必要性.
参考文献:
[1]刘思峰,郭天榜,党耀国,等.灰色系统理论及其应用[m].北京:科学出版社,1999.
[2]王学萌,张继忠,王 荣.灰色系统分析及实用计算程序[m].华中科技大学出版社,2001.
[3]王 炜,等.道路交通工程系统分析方法[m].北京:人民交通出版社,2004.
[4]陆传赉.排队论[m].北京:北京邮电大学出版社,1994.
[5]林元烈.应用随机过程[m].北京:清华大学出版社,2002.

