摘要:通过对城市轨道交通列车实际运行不确定性的分析,提出城市轨道交通追踪列车间隔时间是由最小列车间隔时间和平均必要缓冲时间两部分组成。应用概率论和排队论,给出城市轨道交通高峰期线路通过能力的动态不确定型计算方法,使城市轨道交通系统能不断适应列车晚点的变化。
关键词:城市轨道交通;通过能力;晚点;缓冲时间
引言
城市轨道线路通过能力的固定型计算方法,对于追踪运行时间一般只考虑区间运行时间、制动时间、停站时间和列车加速出站的时间,往往忽略了由于车辆、信号、牵引、运营、线路等各种情况变化而造成的列车延误对通过能力的影响。这样得到的通过能力只有在“严格”按图运行,设备无故障,工作不中断等条件下才是正确的。但事实上列车延误、设备故障在所难免。因此,用定型方法计算的通过能力一般偏大,在高峰期间用它来指导工作必将导致列车晚点增多、运输秩序混乱、运输质量下降。平均最小列车间隔时间计算法属于动态的不确定型计算方法,它是在分析研究当前实际列车运行状态的基础上,依据列车进入晚点概率、时间和平均最小间隔时间的取值等因素,按给定反映列车运行工作质量要求水平的允许列车后效晚点时间总值等条件来计算通过能力的方法。
1线路通过能力的基本计算
城市轨道交通采用自动闭塞,列车追踪运行。考虑到车站一般不设置配线,列车在正线上办理客运作业,列车停站时间是影响轨道通过能力的重要因素之一。在计算轨道固定技术设备的通过能力时,没有必要再去分别计算区间通过能力和车站通过能力,而应该把车站和区间看作一个整体予以综合分析,来计算其线路通过能力。
线路通过能力计算公式可表示为:

城市轨道交通追踪列车间隔时间的确定,应考虑列车停站时间,行车组织方法等的影响。在理论上它取决于同方向列车间隔的距离、列车的运行速度及信号、联锁闭塞设备的类型。
2追踪列车间隔时间的组成
解决追踪列车间隔时间的计算问题是计算城市轨道线路通过能力的关键。列车晚点对“按图运行”会造成一定程度的影响。由于追踪列车时间间隔概念上没有给两追踪列车留出间隙,以作为恢复晚点延误的空当,使系统不能适应列车晚点的变化。在确定追踪列车间隔时间时考虑由平均最小列车间隔时间和平均必要缓冲时间组成,使得可以机动地调整运行图,避免由于列车延误而导致行车混乱。
2.1平均最小的列车间隔时间
列车最小间隔时间是保证车站能完成必要的接发列车作业和确保列车在区间内安全运行的时间,是按追踪运行列车先后经过车站必须保持的最小空间间隔而得到的。
由于列车是以排队方式进站停车办理作业,是把车站和区间作为一个整体进行研究,计算最小列车间隔时间的最小空间间隔应在当前行列车出清了闭塞分区,在确保行车安全的条件下,续行列车以列车运行图规定的速度恰好位于某一通过信号机或闭塞分区分界点的前方。如图1所示,续行列车从初始位置至前行列车所处位置,须经历进站运行、制动停车、停站作业和加速出站四项作为过程。
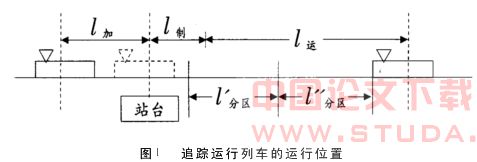
i=t运+t制+t站+t加………………(2)
式中:t运———列车从经过某一通过信号机或闭塞分区分界点时起至开始制动时止的运行时间
t制———列车从开始制动时起至在站内停车时止的制动时间
t站———列车运行图规定的列车停车时间
t加———列车从车站起动加速时起至出清车站闭塞分区时止的时间
平均最小列车间隔时间是指运行列车组最小列车间隔时间的平均值。设根据列车运行图查定的类别运行列车组数为nij,而相应的最小列车间隔时间为iij,则全部列车占用区间的总时间应为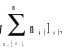 平均最小列车间隔时间i-应为:
平均最小列车间隔时间i-应为:

式中i———运行列车组第一列车的列车种类组序号
j———运行列车组第二列车的列车种类组序号
m———列车种类组数
n———区段运行列车组总数
2.2平均必要的缓冲时间
在具体施画列车运行图时,由于受到通过能力等条件的影响,列车运行图实际安排的列车间隔时间往往大于最小列车间隔时间。把列车运行图规定的列车间隔时间与最小列车间隔时间之差定义为列车运行图缓冲时间。在允许产生一定数量列车后效晚点时间条件下,列车运行图应具有的平均缓冲时间,称为必要运行图缓冲时间。
按照城市轨道交通运行列车组的组成原则和城市轨道交通运行列车组密集排列、运行速度基本一致的情况,在列车运行调度工作中运行列车组按相同等级处理。假定该区段调查期间出现列车进入晚点的列车数为nt,晚点时间总值为t,据此参数g(列车进入晚点的概率)应为:
g=nt/n……………………(4)
每一运行列车的平均进入晚点时间t-表示为:
t=t/n……………………(5)
在给定列车后效晚点时间总值的情况下,每一具体区间的缓冲时间应为:
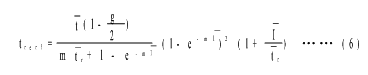
式中:t-——运行列车平均进入晚点时间(秒)
i-——运行列车组平均最小列车间隔时间(秒)
tr-——平均列车运行图缓冲时间(秒)
m——列车晚点概率密度函数参数
3高峰期线路通过能力的计算
城市轨道交通高峰期线路通过能力的计算公式可表示为:
n=3600/(i+trerf)(列/时)…………(7)
式中,对列车的追踪运行间隔时间作了补充,加入了平均必要运行图缓冲时间,为晚点延误提供恢复余地。由于较小的时间间隔就意味着较大的运输量,如果系统没有运营裕量,延误就会持续到高峰期结束。这种计算方式充分考虑了由于旅客上、下车,列车线路本身等原因造成的延误而留有裕量,可以有效缓解未能“按图运行”造成的列车行车无序状态,使得以快捷、高效的方式使轨道线路恢复正常行车。通过对现有城市轨道交通运行图和列车晚点时间的统计、分析和计算,确定在比较繁忙车站运营裕量一般为15s左右。
4结论
城市轨道交通通过能力平均最小列车间隔时间计算法是以概率论和排队论为理论基础,以保证实现一定列车运行工作质量要求为决策依据所建立的方法。它的计算结果表现为在一定主、客观条件下可实现的通过能力。这种计算方法充分考虑到了列车晚点带来的影响,引入了列车运行图缓冲时间的概念,使运行图成为具有一定调整余地和应变能力的柔性运行图,在实际工作中更具可行性。
参考文献:
[1]胡思继.铁路行车组织.北京:中国铁道出版社,1998.
[2]季令,张国宝.城市轨道交通运营组织.北京:中国铁道出版社,1998.
[3]毛保华等.城市轨道交通.北京:科学出版社,2001.
[4]张国宝.地下铁道通过能力计算方法的探讨.上海铁道学院学报,1995.3.

