摘 要: 从理论上分析了影响重庆轻轨票价的主要因素,提出用拉姆齐(ramsey)定价模型和“高峰负荷定价法”确定介于边际成本和盈亏平衡之间的最优票价。同时运用计量经济学的方法对轻轨价格需求弹性系数和运营成本做了近似估计,并为重庆轻轨制定出分段计程制票价方案。
关键词:轻轨;定价;拉姆齐模型;城市轨道交通
重庆轻轨较新线是重庆市重要基础设施,对于这条轻轨如何充分考虑各种因素,制定出既符合社会效益又满足企业正常运转的合理票价是个复杂的问题。国内现有的研究大多侧重于定性分析,而相关的定量分析较少。因此,拟通过拉姆齐(ramsey)数学模型对制定轻轨票价进行定量分析。
拉姆齐模型作为非线性定价模型,在国外已经被广泛应用于交通、电信、电力等行业的定价[1]。为此将拉姆齐模型应用于重庆轻轨票价的制定,为国内城市公共交通,特别是轨道交通的定价提出一种新的思路和方法。
1 影响轻轨票价的主要因素
(1)轻轨成本。成本是影响票价制定的主要因素。重庆轻轨较新线总投资45亿元,固定成本与运营成本都十分庞大,因此仅仅依据成本来制定票价,将大大超出旅客的承受能力。
(2)公众的承受能力。重庆处于西部欠发达地区,2003年重庆市城市居民人均可支配收入为8 094元。通过对居民消费结构的统计分析,按交通费用占居民收入平均比例为15%计算,居民全年人均交通费用为 1 214 元,则平均日交通费支出为 3.33 元,该数据可做为制定合理的轻轨票价的参考。
(3)其他公共交通工具的竞争问题。重庆是著名的“山城”,根据重庆市居民出行调查显示,由于受地形、城市布局等影响,公共交通占居民出行方式的55.3%。目前重庆市普通公交车的平均运价率在0.1~0.2元/km之间。从缓解城市交通和维护轨道公司自身利益考虑,轻轨的票价与其他公共交通的票价应有合理的比例,这样既能体现轻轨方便、快捷和环保的优势,又能吸引大部分客流,从而创造可观的经济效益和社会效益。
(4)政府补贴问题。目前世界上至少有2/3的轨道交通需要政府的运营补贴。因此对于轨道公司在客流少的运营时段的损失和低价运营的亏损,政府要通过财政补贴或减免费用等手段加以弥补,使企业能够维持正常的运营。
2 拉姆齐模型及计算方法
综合以上分析,重庆轻轨由于巨额的固定成本,导致其平均成本要比边际成本高很多,如果采用边际成本定价,企业会出现巨额亏损,还将导致轨道交通过于拥挤(降低舒适度)和诱发事故;如果采用盈亏平衡定价,又会超出普通居民的承受能力,达不到承担交通分担率的目标。所以应选择一个介于边际成本和盈亏平衡之间的票价水平。
而介于边际成本和盈亏平衡之间的最优票价水平可由拉姆齐定价模型确定。其表达式为:

式中:p为价格;mc为边际成本;e为价格需求弹性系数;a为拉姆齐指数。
从公式⑴可以看出,拉姆齐定价模型正是考虑在边际成本基础上的一个加价(mark-up)。当市场存在高峰和非高峰时段差别时,令pi、mci和 εi(i=1,2)分别代表高峰和非高峰时段的价格、边际成本和价格需求弹性系数,则将⑴式变形为:
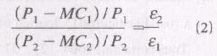
公式⑵是拉姆齐模型的高峰负荷定价法(peak-load pricing),即消费者在高峰时段对于价格的敏锐程度明显小于非高峰时段。根据公式⑵,企业可以采取在高峰时段定高价,而在非高峰时段定低价的策略[2]。因此最优票价水平就可借助“高峰负荷定价法”来求解。
假设企业在所有时段(不考虑与式系运的峰和非高峰时段的差别)制定单的盈亏平衡点票价p,与之相对的边际成本和价格需求弹性系分别为 mc 和ε,再根据非高峰段的边际成本mc2和价格需求性系数ε2,利用公式⑵便能求出高峰时段的票价p2(<p)。由于市交通最拥挤和繁忙是在高峰段,那么政府用非高峰时段的票p2代替盈亏平衡点票价p,便能最大限度的对城市交通的客流,别是高峰时段的客流进行疏导。
3拉姆齐模型的应用
由于城市轨道交通在所有时的边际成本变动很小,故⑵式可写为:
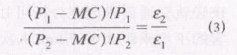
据此制定出重庆轻轨的计程价方案。
3.1 轻轨价格弹性系数的确定
从文献[3]可知,传统确定需弹性系数的方法有两个:①建一个适合于自身交通系统特点需求弹性模型;②采用著名的impson-curtin法则,假设需求弹系数恒为-0.33,即票价每提高10%,客流量会减少3.3%。
如采用ols方法估计需求弹,设交通行业年客流量q(人次)平均票价p(元)满足函数关系:
q=a pε
试中:a为常数; ε 为价格需求弹性数。对上式两边取对数得:
ln q=ln a+ε ln p
由于重庆轻轨2005年才正式营,因此可以根据类似条件轻轨历史数据作线性回归,估计出e。取的城市应该具备与重庆市类公车的条件:
(1)地形地貌特征相似;
(2)百万人口以上的大城市;
(3)交通出行方式相似。
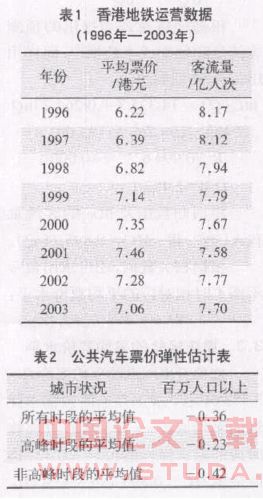
在比较北京、上海、广州和香等相关城市后,选择香港作为参城市。因此,选取香港地铁1996—2003年的运营数据作线性回分析(见表1)[4]。
用eviews3.0回归可得:
lnq= 21.235 0 - 0.389 3 lnp 检验:(271.362 6)(-9.652 346) r2=0.939 5 e=0.000 3.w=2.430 2 f 检验:93.167 8
根据文献[5],公共交通(普通交车、地铁、轻轨等)的需求弹性数在-0.2~-0.5之间,且普通交与城市轨道交通的需求弹性有“相似性”,故把e的值与美国共交通协会公布的美国公共汽票价弹性(见表2)做比较,资料来源于美国公共交通协会网站[3] 。由表2可知e的估计值是符合实际情况的。
以上估计出来的 e 显然是所有时段的平均值,而由于在非高峰时段存在购物流、旅游流等因素,城市轨道交通的需求弹性和公交车基本相同[5],因此可以把表 2 中的e2=-0.42 作为轻轨非高峰时段的需求弹性值。
3.2 重庆轻轨成本分析
按照经济学原理,轻轨运营成本c与客流量q满足函数:
c(q)=bqe ⑷
式中: b、e为常数。
在生产规模不变(固定成本不变)的情况下,边际成本实际上就是运营成本对客流量的导数,即将⑷式两边取对数,得:

将回归数据及相应的客流量代入⑸式,得: mc=0.895 7(元)。
根据相关数据,还可求出盈亏平衡点时相对应的平均票价水平:
p=3.383 6≈3.4(元/人次)
3.3 重庆轻轨的平均票价水平
把盈亏平衡点的平均票价 p=3.383 6(元/人次),所有时段需求弹性的平均值e=-0.389 3,非高峰时段的需求弹性值e2=-0.42,边际成本mc=0.895 7带入公式⑶:
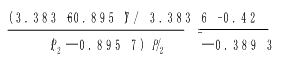
即为重庆轻轨的平均票价水平。
3.4 重庆轻轨票价方案制定
纵观世界各国的轨道交通系统,几乎60%以上都采用的是计程票价制,因此重庆轻轨如采用分段计程票价制,根据文献[7]中介绍的相关方法,具体步骤如下。
(1)重庆轻轨的基本票价。在充分考虑重庆市居民承受能力,并参照北京地铁相关经验的基础上,采用基本票价p*为平均票价p2×30%的方案,即:
p*=p2×30%=2.81×30%≈1(元)
(2)重庆轻轨的运价率。由重庆轻轨交通需求调查分析可知,乘客的平均乘距为6.67 km/人次,根据运价率=(平均票价-基价)/平均乘距,可算出运价率为:
v=(2.81-1) /6.67≈0.27(元/km)
按照票价进制取整的原则,计程区段长度为1/v 即3.7 km,换算成乘车区间则为每4个乘车区间为一个收费区段。
(3)重庆轻轨计程区段。采用按实际乘距,逐渐增加优惠的策略,这也是非线性定价的核心思想。因为轨道交通与普通公交车相比,其短途客流(1~5站)的平均运价率相对较高,显然对长距离乘客具有较强的吸引力,因此在制定计程票价方案时,应考虑尽可能多的吸引中长途乘客。同时根据重庆轻轨交通需求调查分析,62.4%的受访者选择起步价为2元的票价方案,考虑到以上因素,最后制定出的票价建议方案见表3。

考虑到轻轨的客流主要是转移乘坐公交车的乘客,所以票价就不能比公交车高太多。又由于乘客的平均乘距为6.67 km/人次,即绝大部分的乘客在7、8站以内,所以对于大部分中短途的乘客来说 2~3元的票价是具有较强吸引力的。而对于超过8 km行程的乘客,票价提高10%,客流仅减少1%,因此该票价方案不会对长途乘客产生较大的影响。
参考文献:
[1] wilson.r.nonlinear pricing[m].ox-ford university press, oxford,1992.
[2] 杨君昌,曾军平.公共定价理论[m].上海:上海财经大学出版社,2002.
[3] american public transportationassociation.fare elasticity and it's ap-plication to forecasting transit demandabstract [eb/ol]./research/info/online/elastic.cfm, 1991.
[4] 香港地铁有限公司.香港地铁2003年年报 [eb/ol]..hk/chi/investors/2003frpt_c/f120_c.pdf,2003.
[5] litman, t.transit price elasticities andcross-elasticities[j].journal of publictransportation,2004,(2):37-58.
[6] 陈义华,赵良杰,车天义,等.重庆轻轨较新线票价制定总报告[r].重庆市轨道交通总公司,2004.
[7] 蔡顺利,蒋玉琨.北京地铁计程票价方案探讨[j].交通运输系统工程与信息,2002,(3):44-47.

