摘要:对城市轨道交通双导线接触网悬挂风载体型系数进行了计算选用方面的探讨,并对接触线风偏移、计算跨距、支柱挠度和计算荷载的影响进行了分析,建议多导线的风载情况应考虑导线间的屏蔽作用。
关键词:城市轨道交通; 接触网;双导线;风载体型系数;选择
随着上海、广州、深圳、南京等城市地铁轻轨交通的建设和运营,城市轨道交通架空接触网在借鉴国外地铁接触网成功经验的同时,又密切融合了我国干线铁路架空接触网的技术优势,取得长足发展。较之于交流25 kv 接触网,城市轨道交通采用直流1 500 v 供电制式,为适应低电压大电流的需要,其接触悬挂一般由双接触线和双承力索或单承力索以及1 根或2 根辅助馈电线组成。众所周知,接触网无论是直流还是交流,都必须考虑由风引起的荷载对接触网设计的影响。一般来讲,接触网设计计算一是校验在风最大的情况下接触线的风偏移是否在受电弓滑板的允许工作范围之内,着重反映在确定计算、选用跨距和确定拉出值等方面;二是要计算确定接触网支持结构的最大荷载,着重反映在确定支柱的最大工作荷载、基础荷载等方面。其中,悬挂线索的风载确定十分重要,我国《铁路电力牵引供电设计规范(tb10009-98 )中规定了干线铁路单接触线和单承力索情况下线索的风载计算公式及相关参数。而直流接触网一般由平行悬挂间距为40 mm 的2 根接触线和承力索组成,在风的作用下,2 根导线由于线夹的固定,将产生上风侧线材对下风侧线材的屏蔽作用,在具体计算中应将这2 根线索按照一个整体计算,即提出了在计算中如何选用和确定2 根线索的风载体型系数问题。本文拟结合我国的有关规定,参照前苏联、德国关于系数对最大计算跨距和支柱荷载影响的分析以及日本国铁中对风载体型系数的选用,并通过不同体型就直流接触网风载计算中如何确定和选用适当的风载体型系数进行探讨。
1 悬挂线索风载的计算
接触网悬挂导线包括接触线、承力索、架空地线和附加导线等,当风垂直吹向线索时,线索承受的风载最大,根据伯努利定理,线索上承受的风载表示式为p = acv2/16 , (1) 式中,p 为线索上承受的风载,kg;a 为受风面积,m2;c 为风载体型系数(亦称阻力系数);v 为设计风速, m/s 。若以线索的直径d(mm)表示,其单位风载p′= cdv2/16×103 , (2) 单位为kg/m。由式(2)可见,当设计风速和线索直径确定后,影响线索风载大小的主要是风载体型系数c。风载体型系数是与受风导体形状有关的参数,如果是相似的受风导体,则与受风面积无关。
tb 10009-98 中规定:在单线情况下考虑承力索和接触线通过吊弦的相互作用,链形悬挂的线索风载计算的风载体型系数按1.25 选用,简单悬挂和单附加导线则按1.2 选用;对双导体悬挂情况,一般双接触线或双承力索的在悬挂点平面内以40 mm 的间距布置,并通过吊弦线夹连接,当风以一定的迎风角α(风与2 根线索的中心连线的夹角)吹向双导线时,情况与单导线时有所不同,在风的作用下,2 根导线间将产生缓冲风压的屏蔽影响。如图1 所示。
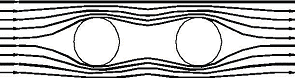
图1 2 根导线产生的缓冲风压的屏蔽影响
基于如上原因,各国在考虑双导体的风载体型系数方面有所不同。我国《66 kv 及以下架空电力线路设计规范》(gb 50061-97 )第7.1.2 条中规定的风载体型系数:d<17 mm 时取值为1.2; d≥ 17 mm 时取值为1.1;覆冰时取值为1.2。对分裂导线,不应考虑线间的屏蔽影响。德国接触网双导线计算风载时,按每根单导线的风载乘以导线的根数进行计算。前苏联则规定了支柱位于路面、路堑和5 m 以上路堤情况下的双线风载体型系数的不同取值,见表1。
表1 双线风载体型系数的取值
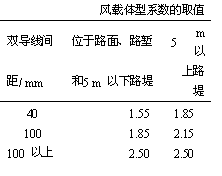
日本通过的风洞试验结果如下:2 条成束组合的馈电线或单线的风载体型系数为0.96 ;而在2 条线紧靠且迎角α = 0°时,风载体型系数为0.37~0.45;迎角α=90°时该系数为单线情况下的125%。对间距为100 mm 的双接触线和间距为50 mm 的双承力索进行风洞试验时发现,当迎角α=10° 时,线的干涉(屏蔽影响)则不复存在。通过风洞试验得出了如下基本结论:一般在多导线情况下,线间距离导致其风压比单线风压要小,这是由于下风侧导线所受到的风压减小的缘故。同时由于下风侧导线的影响,上风侧导线受到的风压也减小了几个百分点。由此,日本在计算双导线的风载时,风载体型系数比单导线情况要小些。
在我国现有的设计规范中只规定了单根线材的风荷载体型系数,而对双根线材、多导线的风荷载体型系数没有明确规定。在实际的设计中,多根线材风荷载的计算是将单根线材的风荷载系数
(1.25)乘以线材的根数,但这样计算忽略了并排导线的屏蔽影响,计算结果偏大,影响了支柱的设计、选用。因此在今后的设计中,应考虑并排接触线风载屏蔽的影响。
2 接触线风偏移和计算跨距的影响
接触线调整水平面内安装应保证在受电弓的许可工作宽度之内。接触线的偏移则主要考虑了拉出值、最大风偏移、机车车辆的摆动、受电弓的晃动、腕臂偏移量以及线路的曲线超高等因素。显然,在拉出值一定的情况下,风偏移是决定因素,而设计参数主要是确定最大跨距值和选用跨距。接触线的最大许可偏移和跨距之间的关系,由式(3)和式(4)确定。
在直线情况下:
bmax = b0+a2/4b2+γ, (3)
在曲线情况下:
bmax = b0 + l2/8r - a +γ, (4)
式中:bmax 为接触线最大允许偏移值,mm ;b0 为风载偏移值,mm;a 为拉出值,mm;r 为曲线半径,m;γ为导线悬挂高度处支柱的挠度,一般钢支柱为50 mm ,混凝土支柱为20 mm 。
我国计算链形悬挂风偏采用了当量系数法,而前苏联和德国则都采用了加入吊弦作用后的风载计算法。研究和计算表明,在接触线张力和拉出值确定后,接触网的允许最大跨距随风载的增加而减小。现将采用单导线风载体型系数乘以导线根数的城轨交通接触网双导线风载体型系数的选用计算法与前苏联风载体型系数算法进行比较,当最大允许风偏为375 mm 时,最大允许的计算跨距如表2 所列。
表2 最大允许的跨距计算值
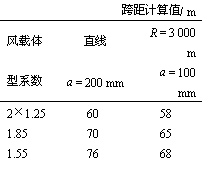
由表2 可知,随着风载体型系数取值的减小,计算允许的最大跨距将增大5~10 m。在实际工程中,考虑裕量后,选用跨距亦可增大1~2 个等级。跨距的增大,实际上会引起支柱容量的增加,虽然平面布置的裕度大了,但支柱的价格也相应增加。故而,风载体型系数的选用还应结合对支柱挠度和计算荷载影响后综合考虑。
3 支柱挠度和计算荷载的影响
在接触网支柱的设计中,直线区段上,风荷载占支柱的总荷载的比例最大时可达到60%左右。其中支柱形体所产生的风荷载一般为线索产生风荷载的10%左右。因此,接触网线材的风荷载体型系数的选用尤为重要。
链形悬挂的双导线按2×1.25 ,较前苏联采用的1.85 和1.55 分别提高了35 % 和61.2 % ,风荷载的提高是显而易见的。以一直线腕臂柱为例,采用上述3 种体型系数,其计算条件和结果如下。
(1)计算条件:
最大风速为35 km/h ;柱高为7.0 m ;跨距为50 m ;接触线(2 根)悬挂高度为5.1 m ;承力索(2 根)悬挂高度为6.2 m ;架空地线(1 根)安装高度为6.4 m ;馈电线(2 根)安装高度为5.9m。
(2)纯风作用于垂直线路时,柱底荷载和柱顶挠度的计算结果如表3 所列。
表3 中的计算结果未考虑悬挂重量、导线横向力、检修重量等情况引起的荷载。可以看出,导线作用于支柱底部的弯距值,风载体型系数为1.55 时比2×1.25 时降低约30%,柱顶挠度降低约33%。
表3 柱底荷载和柱顶挠度的计算值

上述计算结果与支柱的结构和选型有关,如圆锥形钢管柱的壁厚可适当减小,则支柱重量减轻,制造简单,也更为经济,同时在城市轨道交通的高架桥上架设架空接触网时也将相应降低对高架桥结构承载体的荷载要求。
4 结论和建议
通过风载体型系数的选用对计算跨距和支柱荷载及挠度的影响分析,可知双导线风载体型系数的取值对接触网平面布置中最大跨距及支柱荷载有着显著的影响。采用单根导线风载体型系数乘以悬挂导线根数的算法,接触网允许的跨距值变小,风载引起的支柱荷载和挠度变大。从设计和施工安全的角度考虑,安全系数变大了,但从工程经济的角度考虑则不利于节省投资。鉴于我国设计规范对双导线悬挂的接触网线材风载体型系数没有明确规定,参考日本和前苏联设计采用的风载体型系数值,建议对多导线的风载情况应考虑导线间的屏蔽作用,采用前苏联的风载体型系数较为合理,不过还应结合我国城市轨道交通接触网工程的实际特点、有关风洞试验结果和工程实践,确定适合我国城市轨道交通双导线悬挂风载计算采用的风载体型系数值。
参考文献:
[1] 符拉索夫. 接触网 [m].
[2] 电气化工程局科技信息中心编译.日本电气设施设计施 工标准[m].
[3] 德国铁路规范.ds 997.01. 接触网设施的设计、施工和维修[s].

