摘要:合理的冷藏库气体流场,可以保证冷量的均匀分配,保证冷藏食品品质。近年来,计算流体力学(cfd)技术随着计算机科学和流体力学理论的发展而在工业各领域得到广泛使用。本文中,作者利用cfd技术对一实际水果冷藏库流场进行了数值模拟,并通过实验验证了模拟的可靠性。研究表明数值模拟在冷藏库流场优化设计中应用切实可行而且优势显著。
关键词:计算流体力学 冷藏库 数值模拟 实验验证
1 引言
合理的冷藏库气体流场,可以保证冷量的均匀分配,节约能耗,降低干耗损失,提高货物质量。据调查,目前大多数冷藏库的气流组织欠合理,这是由于冷库大多是凭经验设计建造的。为了获取冷藏库内流场的信息,传统的方法是进行实验测量或作流场可视化研究。这些做法在实际运用中都具有很大的局限性,使用成本也很高,而且也不可能获得整个流场内详尽的信息。计算流体力学(computational fluid dynamics,简称cfd)是在经典力学,数值计算方法和计算机技术基础上建立起来的新型学科。它通过建立数学物理模型,根据提供的边界条件和参数,可以对速度场、温度场、压力场等诸多物理量进行仿真模拟,从而提供流动区域内精细的流场、温度场,因而通过cfd研究可以更好地分析冷藏库内流体的流动情况。
近年来,数值计算技术在食品、制冷等工程实际中得到了广泛的应用,并取得了相当满意的效果,然而文献检索发现,将数值计算应用于冷库方面的研究却是很少。瞿晓华等人利用cfd技术对一小型装配式冷库流场进行数值模拟,分析了流场形态及各种设计参数对冷藏库内流场的影响。研究表明数值模拟在冷藏库流场优化设计中应用切实可行而且优势显著 [1];王剑锋等人对分别属于两个冷库的流场进行了二维模拟研究,并对气流组织进行了对比分析,指出冷库流场存在一个中心大回流,流场的主流有靠近边界流动的趋势,无论是水平还是垂直速度均呈现两边大、中间小的格局[2,3];胡浩等人建立了水果气调库库内气体流动、传热和传质的非稳态数学模型,还根据水果的呼吸原理建立了货物区的传热、传质控制方程,采用simple算法和整体求解的解法对水果气调库的降温、降氧等非稳态过程进行了数值模拟,但最后的计算没有作进一步的验证研究[4]。总之,数值计算在冷库中的应用不多,且基本上处于模型设计的阶段。
本文对属于江浦冷冻厂的一个果品冷却物冷藏间进行了流场实测和数值模拟计算,其中模拟计算主要利用商用cfd软件fluent来得到三维流场结果,对模拟结果与实测值进行了比较,取得了较好的一致性,误差在允许范围内,表明了数值模拟在冷藏库气体流场设计中应用的可行性。通过本文的研究,期望对冷藏库的流场设计和改造具有一定的参考价值。
2 物理及数学模型
2.1 物理模型
本文中所研究的冷库为上海市江浦冷冻厂的一个果品冷藏库,该库的的内型尺寸为26.93m(长)×12.76m(宽)×3.8m(高),空气冷却器为两台lff型8#轴流风机,每台风量33000m3/时,转速1450转/分,功率4kw,风机位于墙内,通过一均匀送风道将冷量送至冷库,该风道位于冷库中部,离地高1.96m,送风道高为44cm,两边对称各突出20个圆柱状送风口,冷库两边堆放货物,货物为苹果。本研究中为简化起见,将货物看成两贴壁的长方体,按照冷库内实际情况,设定每个长方体尺寸为26.93m(长)×3m(宽)×2.4m(高),冷库及货物堆放情况由如图1所示:
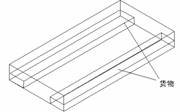
图1 冷库及货物堆放示意
2.2 数学模型
为了取得数值模拟的结果,首先要建立合适的描述冷藏库内流动换热的数学模型,先做如下假设:
1) 冷藏库内空气为不可压缩的理想气体;
2) 冷藏库内管道和铁架等支承物对流场没有影响;
3) 流场为不随时间变化的稳态流动。
冷藏库为有限空间强制对流,流场re约为106,处于紊流状态,结合上列假设,采用d.b.spalding的紊流流场k-ε的数学模型[5],在直角坐标系下,联立连续性方程,动量方程,k方程,ε方程及能量方程作为计算方程组,该方程组可以用下面的通用微分方程形式表示:
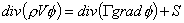
式中:φ-通用变量;г-与φ相对应的广义扩散系数;s-与φ相对应的广义源项。不同方程对应关系见表1 。
表1 各控制方程变量、扩散系数及源项
table 1 variables, diffusion coefficients and source terms of each governing equations
方程
φ
γ
s
x方向动量方程
u
η+η
t
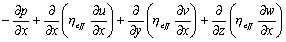
y方向动量方程z方向动量方程
vw
η+η
tη+η
t
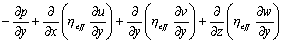
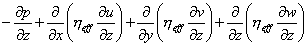
紊流能量方程
k
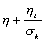
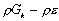
紊流能量耗散方程
ε
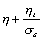
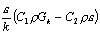
能量方程
t
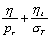
0
表中: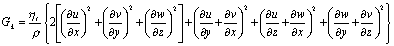
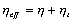 ;
; 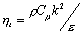
k-ε模型中经验常数采用经典推荐值(见表2)。
表2 k-ε模型中的系数
table 2 the coefficients in k-εmodel
c
µ
c
1
c
2
σ
k
σ
ε
σ
t
0.09
1.44
1.92
1.0
1.3
0.9~1.0
2.3 边界条件
本文采用的k-ε模型属高re数模型,适用于离开壁面一定距离的紊流区域。但由于在贴近壁面的粘性底层中,紊流re数很低,这就必须考虑分子粘性阻力的影响,故采用在工程计算中应用最多的壁面函数法来处理。入口边界采用速度边界条件,由风速仪及热电偶测得入口平均风速为8.9m/s,温度为275k,由于k,ε难以测量或计算,采用紊流强度与特性尺寸来定义紊流,紊流强度是指脉动速度平方时均值的方根与某一特征速度的比值[6],本研究中设为5%,由于送风口为圆形,因此水力直径为圆直径0.11m,出口边界采用压力出口条件,出口压力及温度皆设为环境值,出口风速由软件自行计算得到,壁面边界采用第一类边界条件,经热电偶多次测量,取其平均值4℃(277k)为壁面温度,速度情况按无滑移条件处理,即壁面各方向速度为0。
2.4 货物的处理
在本研究中,根据冷库内贮藏的货物及其堆放方式的特点,将其看作多孔介质处理。苹果视为球形固体颗粒,间隙中的气体对应于多孔介质中的流体。由于货物箱壁的障碍以及货物区多孔结构所造成的极大的流动阻力,货物区中的气体流动极其微弱,其大小和分布对冷库内气体主流区的影响可以忽略,因此可近似认为货物区中气体流速为零。[4]
由于本研究最终需要得到冷库的温度场分布情况,因此对于货物区,需要知道其热导率,由文献[7],j.c.maxwell提出以电热模法获得多孔介质的有效热导率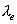
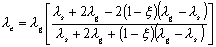
式中:下标g,s——气体,固体,ξ——多孔介质的孔隙率。
上式适用于球形颗粒多孔体且ξ值较高的场合。苹果热导率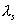 为0.418 w/m•k[8];空气导热系数按0℃时选取kg=0.0244 w/m•k[9] ,根据实际情况,假设每箱苹果中苹果总体积占箱体积的一半,ξ设为0.5,则货物区当量导热系数
为0.418 w/m•k[8];空气导热系数按0℃时选取kg=0.0244 w/m•k[9] ,根据实际情况,假设每箱苹果中苹果总体积占箱体积的一半,ξ设为0.5,则货物区当量导热系数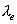 经计算得0.0772w/m•k。
经计算得0.0772w/m•k。
苹果的呼吸热是冷库内的主要热源,不可忽略,据资料查得苹果0℃时的呼吸强度为v0=2.24ml/kg•h,呼吸热为q0=12.1w/t ,假设货物区平均温度为3℃(276k),则苹果的呼吸热按简单插值计算得15.48 w/t=12.384w/m3,苹果密度选为800kg/m3。[10]
3 计算及结果分析
本研究中前处理采用gambit软件进行几何建模及网格划分,采用copper方法划分网格,在送风口及壁面处将网格局部加密,为使结果准确,网格步长设为0.25,一共生成约550,000个网格,将网格文件导入fluent,根据上述边界条件及货物情况进行设置,采用控制容积法对控制方程进行离散,再用simple进行流场计算,收敛精度除能量方程为10-6外,其余方程都设置为10-3,计算结果分析如下。
由于计算结果的三维显示只能看到库壁面的参数分布情况,无法清晰显示库内尤其是货物附近的流场分布情况,因此本研究将在三维库中选择有代表性的切面,分析切面上的参数分布来进行研究。
图1为经过某两个对称送风口的截面上的速度分布,两边无速度处为堆放的货物。由图可知,速度场以风道为中心呈对称分布,送风口处速度最大,由于货物阻隔,气流在货物处形成分流,分别向上和向下流动,并形成两个涡流区,涡流区内气体速度较小,然而由于货物未贮藏于涡流区,因此对于货物贮藏没有太大影响;货物区受到送风口气流直吹,冷却效果较好;流场在库上部拐角处呈现速度减小的趋势,在速度矢量图中表现为速度的不连续,且存在小漩涡,这可用流量守恒定律解释(a1v1=a2v2 ),因为拐角处流动截面积增大,使该处的流动速度减小;而拐角处的小漩涡是由于壁面的阻碍扰流引起的。
本研究的实验验证选取的是离地高1.1米的等高面,为便于进行实验与理论计算的比较,因此数值计算得到的温度场也用此等高面上的结果表示,见图2,由图可见,温度场呈现均匀化趋势,由于送风口在冷库中部往两边吹风,因此,此区域气体速度较高,温度比较低,并向两边逐渐上升;前文已提及货物区内气体流速为0,加之内热源的作用,温度较高;在库体壁面上,由于流体在库体表面无滑移,加之外界热量的作用,其温度为整个流场最高处,壁面拐角处温度尤显高,是因为存在涡流,不利于散热。
图3为送风口中心等高面上压力场的分布,中间的空区域为送风道,由图可知,送风口处,风速较大因此压力较大,到主流场,压力有所降低,再往两边,在主流区与货物区接界处,由于气体流动受到固体货物的阻扰,加剧了气体的扰动,因此压力也较大,到货物区,由上述气体速度为0,因此压力为0 。
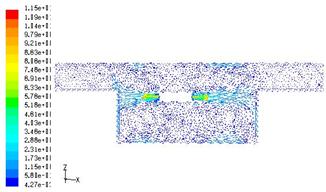
图1 送风口截面处的速度分布
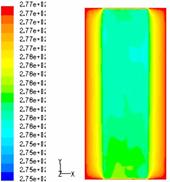
图2 离地高1.1米的水平截面上的温度计算结果

图3 送风口等高面上的压力分布模拟结果
4. 实验验证
为了验证数值计算的正确性,我们在库内离地高1.1米的等高面上布置了30对热电偶对数值计算的温度场进行了实验测试,在布点的过程中,由于货物的堆放,对布点造成了不少的困难,作者尽量在冷库内各区间均匀布点,力争全面准确地反映冷库的温度分布情况,将测得的数据导入绘图软件origin中,通过转换矩阵等工作,绘制出等温图,如图4。由图4和图2的比较,可看出两图的分布特性是一致的,具体各点间温度比较见表1。
表1 库内1.1米等高面上实测值与计算值的比较
序号
实测值(℃)
计算值(℃)
1
3.9
4
2
3.8
4
3
3.9
4
4
2.8
3
5
3.1
3.02
6
3.9
4
7
2.5
2.72
8
2.6
2.76
9
2.6
2.74
10
3.9
4
11
3.8
4
12
3.7
3.78
13
3.5
3.62
14
2.7
2.85
15
2.6
2.77
16
3.0
3.14
17
3.2
3.35
18
2.7
2.81
19
2.9
2.85
20
2.6
2.76
21
2.6
2.76
22
2.8
2.94
23
3.1
3.19
24
2.8
2.89
25
2.7
2.76
26
2.1
2.17
27
2.6
2.73
28
2.6
2.75
29
3.7
3.81
30
3.5
3.63
5. 结论与展望
目前,冷藏库内流场的数值研究极少,且多以研究空库为主。本文运用cfd商用软件对存有货物的冷藏库作了数值模拟,并进行了实验验证,研究表明利用数值计算工具对实际冷藏库流场分析设计是完全可行的。同时,将理论分析、实验研究、数值模拟三者紧密结合起来并相互补充的研究方法也必将大大提高冷藏库的设计水平,改善冷库中的温度场,满足消费者对冷藏食品品质越来越高的要求。
图4 库内1.1米等高面上温度实测图
通过图4与图2的比较以及表1,可以看出实验与理论结果基本吻合,其最大相对误差为8%,在计算允许范围内,说明本研究建立的数值计算模型是正确合理的,能较真实地反映库内实际情况。
参考文献
[1] 谢晶 瞿晓华 徐世琼. 冷藏库内气体流场数值模拟与验证[j].农业工程学报,2005,2:11~16.
[2] 胡熊飞,刘楚芸,王剑锋等.冷库冻结过程气体流场与节能研究[j].制冷,1995,2:5~10.
[3] 胡熊飞,刘楚芸,王剑锋等.冷库冻结间气体流场模拟[j].冷藏技术,1995,4:7~17.
[4] 胡浩,袁秀玲,孙大伟等 . 水果气调贮藏中温度氧组成浓度变化过程三维动态模拟及实验研究 [j] . 制冷学报,1998,1:28-34.
[5] 陶文铨 . 数值传热学(第二版)[m].西安:
西安交通大学出版社,2002,5:347~353.
[6] 陶文铨 . 数值传热学(第二版)[m].西安:西安交通大学出版社,2002,5:344.
[7] m..mariotti,g.rech,p.romagenoni,numerical simulation of air distribuion in a refrigerated room,19th international congress of refrigeration 1995,proceedings volume І.
[8] 谢晶.食品冷冻冷藏原理与技术.化学工业出版社,2005.
[9] 杨世铭.传热学(第二版).高等教育出版社,1987.
[10] 瞿晓华. 气调库的气体流场分析及优化设计[d].上海水产大学:2004.2

