摘 要:介绍电力电子设备的抗震要求,及常用模态求解方法。重点运用ansys进行某框架刚度优化设计的过程,最后结合实验结果对有限元分析加以证明。
关键词:抗震;模态;ansys;有限元
电子电力设备在使用过程中要经受恶劣的环境,在振动环境下,由于振动的疲劳效应及共振现象,可能出现电性能下降、零部件失效、疲劳损伤甚至破坏的现象;特别是户外用电子通讯设备在地震发生时,如能够抵抗地震冲击带来的破坏,则能够在抗震防灾中发挥巨大作用。因此对户外用电子电力设备的可靠性提出了严格要求,要求其具备一定抗振动与冲击的能力。在新产品的设计开发过程中通常用模态分析技术进行结构动态特性的估计以及优化设计。这一过程要得到系统的固有振动特征,然后在给定的使用或振动环境中进行评估,根据结果进行优化。
1 常见模态分析方法
1.1 理论求解法
理论求解是一种传统的求解途径。对于一些理想的简单弹性振动,可以用模态分析理论得到精确解。特别是可简化为单自由度的振动系统可以方便的求解。对于多自由度系统,特别是系统结构复杂,无法进行理想化时,其质量矩阵和刚度矩阵无法通过简单的理论计算来获得,也就无法使用理论法来求解。
1.2 试验法
试验法是最直接的获得系统固有特征的方法。试验装置包括振动台、信号发生器、传感器、信号采集系统、频谱分析仪等。由于其需要实物原形,至少是模型结合相应的试验设备来进行,周期长,耗费较高的人力、物力等资源,很难在普通项目中运用。
1.3 有限元法
有限元法实质上是一种在力学模型上进行近似的数值计算方法。连续体结构体系本身内部不存在自然的连接关系,需要人为地在连续体内部和边界上划分节点,以分片(单元)连续的形式来逼近原来复杂的几何形状。线性有限元法是一种利用位能变分和分割近似原理求解线性弹性力学问题的数值方法。它首先把连续弹性体分割为在节点上相连的单元组合体,然后以节点位移为基本未知量,分别在各单元内选取位移函数,并按线性弹性力学的几何方程、本构方程和虚功方程或位能变分方程,建立并求解关于位移的线性代数方程组,把无限个自由度的问题化为有限自由度问题。随着有限元法的快速发展相继出现了许多有限元法的应用程序,如:ansys、i-deas、adamas等。其中anasys是高校及工程界普遍使用的分析软件。
2 模态分析实例
某户外通信机柜(图1)的骨架由图2所示截面的杆件焊接而成,沿着杆件分布着图3所示的安装定位孔。机柜内部安装通信单元,要求能够在地震多发的环境中使用,在震灾发生时以及灾后要求设备正常工作。
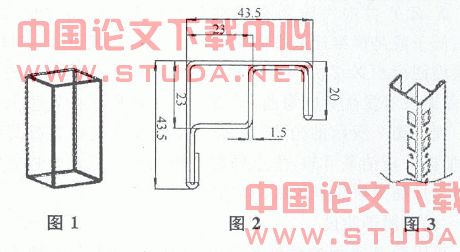
根据iec防灾规范,地震的振动频率主要集中在0.1~35hz,为避开共振产生的破坏,系统的固有振动频率应当尽可能高,特别是避开地震能量集中的低频范围0.1~6hz。下面介绍如何使用ansys来进行固有频率及振型的求解,并根据分析结果进一步优化。
2.1 问题分析
此框架结构虽然是由杆焊接而成,由于沿着杆壁分布着安装孔,不能简化为梁单元。杆件是由薄钢板冲压后滚压成型,根据其截面性质(图2),可使用壳单元。ansys的建模功能相对比较弱,本例首先在pro/e中完成建模,然后读入anasys中。
2.2 前处理
在pro/e中长度单位为mm;为使单位统一,在ansys中用/units命令设置系统参数。长度单位为mm,质量单位为g。在前处理器中设置单元类型为63号壳单元,设置相应的实常数并设置材料属性,泊松比=0.3,密度为 。用modeling>create>glue命令把各梁结合在一起。接下来是网格划分,在modeling>mesh attributes中设置单元号,材料号,单元实常数号;然后使用mesh tool进行网格划分。模态分析对于网格划分的质量要求并不高,可以采用先粗后细的方法来验证。即先用较少的网格数进行分析,再用两倍网格数分析。若两次比较结果差异在可接受范围内即可认为网格划分足够精确。
2.3 加载及求解
对底部的四个顶点施加约束,选择all dof,位移值设置为0。solution>analysis type>new analysis中设置模态分析;在analysis options中设置模态提取方法为reduced法,并设定x为主自由度方向。运行select solve>current ls,保存。接着依次设定y、z为主自由度,运行求解并保存。
2.4 后处理
通过general postproc>read results命令依次读入各自方向的第一阶数据。通过plot results>deformed shape>def+undeformed命令绘制变形图4~图6。

x、z、y方向一阶固有频率分别是8.432,5.798,17.654;低于或是很接近地震能量集中的低频范围0.1~6hz。由振型图可知x、z方向振动模态主要是围绕焊接角点的摆动,而梁没有发生大的弯曲;y方向则是在角点处发生大变形。观察图7所示的角点,它是沿着杆件的接缝直接焊而成,根据分析结果可知,角点局部结构刚度太低。改进方案应当是加强焊接角点的结构刚度。
2.5 优化局部刚度
采用图8所示的角件如图9所示,在每个角点插入角件,然后沿着接缝焊接牢固可起到此作用。
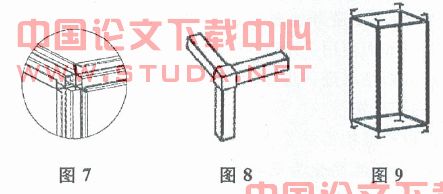
在ansys中导入角件,修改模型,按照2.2~2.4步骤重新分析。得到的x、z、y方向一阶固有频率分别是:12.759,8.946,32.236。改进后的模型各方向上的一阶固有频率明显提高。
3 试验分析
按照改进后的结构制作出框架原形,然后进行振动台测试。用白噪声进行固有频率扫描,获得的各方向一阶固有频率结果如图10~12所示。实验结果与有限元解接近。
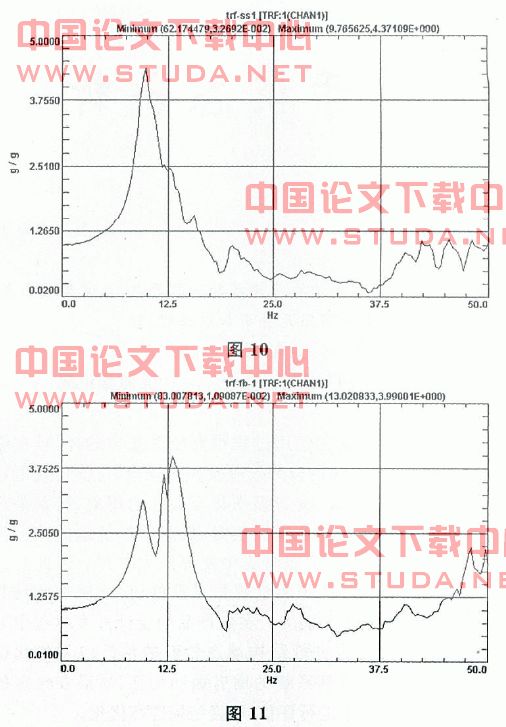
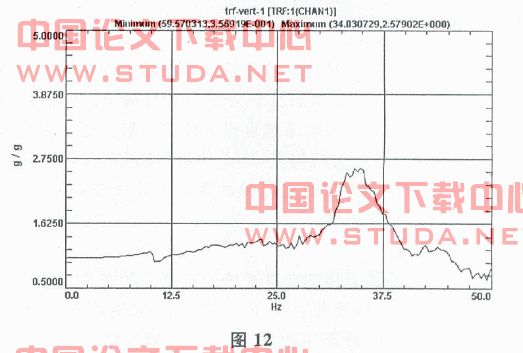
4 结语
通过有限元与模态实验结果的对比,可以看出ansys能够为结构的刚度优化设计提供很大的帮助。并且它不像理论法,不需要烦琐的计算;不像模态实验,不需要昂贵的实验设备以及实验原型。从经济性、费用、可信度等方面来讲ansys不失为一种好的模态分析方法。
参考文献
[1]王勖成.有限元法[m].北京:清华大学出版社,2003.
[2]师汉民.机械振动系统[m].武汉:华中理工大学出版社,1990.
[3]李德葆.实验模态分析及其应用[m].北京:科学出版社,2001.
[4]丰定国.抗震结构设计[m].武汉:武汉工业大学出版社,2001.

