一、引言
电动机调速是各行各业中电动机应用系统的必需环节。直流电动机因其磁链与转矩电流各自独立,不存在耦合关系,能够获得很好的调速范围和调速精度,静、动态特性均比较好而获得广泛应用。
交流(异步)电动机结构简单却因其磁链与电流强耦合,而且是多变量非线性系统,调速难度大,长期以来在调速系统的应用受到限制。直到近三十年来,一系列新型的传动调速技术的出现才开始了交流传动的新篇章。
1.交流传动的发展简述
首先是变压变频调速系统(vvvf),后来出现了矢量控制(foc)和直接转矩控制(dtc)调速系统。由于vvvf系统只是维持电动机内的磁链恒定,并没有解决磁链和电流强耦合的问题,其调速范围窄,调速性能也不佳。矢量控制是以转子磁场定向,采用矢量变换的方法,通过两次旋转坐标变换,实现异步电动机的转速和磁链控制的完全解耦。但实际上由于转子磁链很难准确观测,系统特性受电机参数的影响较大,且计算也比较复杂。
1985年,德国的m.depenbrock和日本的i.takahashi先后提出直接转矩控制理论。直接转矩控制在定子坐标系下,避开旋转坐标变换,直接控制转子磁链,采用转矩和磁链的bang-bang控制,不受转子参数随转速变化而变化的影响,简化了控制结构,动态响应快,对参数鲁棒性好,因而得到广泛的深入研究和应用。
2.矢量控制(foc)和直接转矩控制(dtc)的简略对比
(1)控制原理:foc是在转子磁通坐标系中,通过分别控制q轴和d轴定子电流分量,实现转速和磁链的解耦控制。其实质是通过坐标变换重建的电动机数学模型等效为直流电动机,从而象直流电动机那样进行快速的转矩和磁通控制。dtc是在定子坐标系下通过检测电动机定子电压和电流,采用空间矢量理论计算电动机的转矩和磁链,并根据与给定值比较所得差值,实现转矩和磁链的直接控制。
(2)控制性能:foc的调速范围较宽(1:20~200),调速精度较高,低速特性连续,响应速度较快,但受参数变化影响较大,且计算复杂,控制相对繁琐。dtc的调速范围较窄(1:15~100),调速精度也较高,响应速度快,低速特性有脉动现象,但其不仅计算简便,而且控制思想新颖,控制结构简单,控制手段直接,信号处理的物理概念明确,动静态性能均佳,有广阔的应用前景。
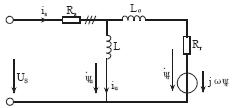
图1异步电动机的空间矢量等效电路
直接转矩控制的基本思想是在准确观测定子磁链的空间位置和大小并保持其幅值基本恒定以及准确计算负载转矩的条件下,通过控制电动机的瞬时输入电压来控制电机定子磁链的瞬时旋转速度,来改变它对转子的瞬时转差率,达到直接控制电机输出的目的。
二、数学模型
1.异步电动机转矩的数学模型
异步电动机的空间矢量等效图如图1所示该等效电路是在正交坐标系(α-β坐标系)上描述异步电动机的。
其中:us(t)-----定子电压空间矢量
is(t)-----定子电流空间矢量
ir(t)-----转子电流空间矢量
ψu(t)----定子磁链空间矢量
ψr(t)----转子磁链空间矢量
ω-----电角速度
则异步电动机在定子坐标系上各方程可表示如下:
电压方程: 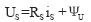 (1)
(1)
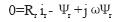 (2)
(2)
磁链方程: 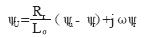 (3)
(3)
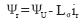 (4)
(4)
转矩方程: 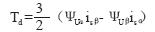 (5)
(5)
若用转子磁链代替定子电流,转矩方程将变成如下形式:
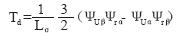 (6)或
(6)或 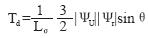 (7)
(7)
θ是磁通角,即定子磁链与转子磁链之间的夹角。
在实际运行中,保持定子磁链的幅值为额定值,以便充分利用电动机,而转子磁链的幅值由负载决定。如果要改变异步电动机的转矩,可通过改变磁通角θ来实现。
2.异步电动机磁链的数学模型
目前磁链模型主要有三种,分别适用于不同转速下应用。
(1)u-i模型
在30%额定转速以上,采用u-i模型,其表达式为:
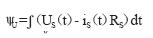 (8)
(8)
从此式可看出,在计算过程中唯一所需了解的电动机参数是易于确定的定子电阻。同样,定子电压us(t)和转子电流is(t)也是易于确定的物理量,它们能以足够的精度被检测出来。计算出定子磁链后,再把定子磁链和测量所得的定子电流代入式(5)就可计算出电动机的转矩。此模型中关键是要准确确定定子磁链,即要求定子电压和定子电阻压降之间的差值存在且误差可忽略,而只有在30%额定转速以上时才能达到这一要求。
(2)i-n模型
在30%额定转速以下,由于定子频率很低(仅有几赫兹),电动机端电压很小,定子电阻rs的变化导致u-i模型中积分项is(t)rs误差较大,故采用i-n模型,其表达式为:
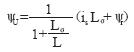 (9)
(9)
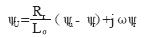 (10)
(10)
在30%额定转速以下范围,磁链只能根据转速来正确计算。在i-n模型中正是用定子电流与转速来确定定子磁链。该模型在这个转速范围内是合适的。但要注意在使用i-n模型时要求准确测量角速度ω,这是因为角速度的测量误差首先引起转子磁链的误差,再由转子磁链的误差引起定子磁链的误差,最终引起转矩误差,故对转速要求有较高精度的测量。
对于u-i模型和i-n模型的应用必须有合理的安排,不同的转速范围应采用不同的磁链模型。
在高速时采用u-i模型,因其模型不仅简单,而且精度也高,受参数的影响小;在低速时采用i-n模型,因为低速时受定子电阻的影响u-i模型已不能正确工作。
(3)u-n模型
由于在由u-i模型向i-n模型切换时,快速平滑切换的困难使得这种解决方案产生问题,而u-n模型是一个在全速范围都实用的磁链模型。u-n模型综合了u-i模型和i-n模型的特点,由上面所提到的转子方程式(10)和定子方程式(1)及磁链方程式(3)、(4)组成。关键在于使用了电流pi调节器,强迫电动机模型电流和实际的电动机电流相等,同时精度大大提高,缺点是结构比较复杂。通过使用u-n模型,解决了u-i模型向i-n模型快速平滑切换问题,并且使电动机在高速时工作在u-i模型下,低速时工作在i-n模型下。
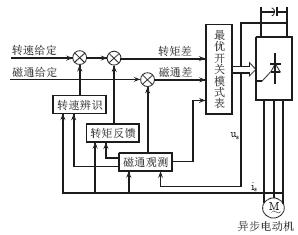
图2直接转矩控制原理框图
3.直接转矩控制的控制模型及控制原理
综合上述的异步电动机转矩和磁链模型,采用直接转矩控制的控制思想,可得到直接转矩控制的控制模型。
直接转矩控制的控制原理框图如下图所示。
由此图可看到控制时需检测出直流母线电压和定子电流,再按下式(11)进行坐标变换到静止的定子坐标系(α,β)上。
其中:xa(t),xb(t),xc(t)是定子相应量的瞬时值, 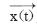 是空间矢量,xα(t),xβ
是空间矢量,xα(t),xβ
(t)是(α,β)坐标系上的两个分量。在α,β方向计算实际的磁通值和转矩值作为反馈分别与磁通给定构成闭环,同时还要计算出磁通所在扇区位置,最终通过转矩差、磁通差、磁通扇区,进行bang-bang控制,利用逆变器的开关特点,通过不断切换电压状态,即不断切换电压空间矢量,使定子磁链轨迹接近圆形,并通过零点压矢量的穿插来改变转差频率,以控制电动机的转矩及其变化率,从而使异步电动机的磁链和转矩同时按要求快速变化。
三、直接转矩控制的缺陷及改进方案
直接转矩控制理论和技术有许多优点,如计算简便,控制结构相对简单,动态响应快,参数鲁棒性好。然而作为一种诞生不久的新理论、新技术,自然有其不完善不成熟之处,有些问题甚至成为它发展难以逾越的障碍。
一个是在低速区,由于定子电阻的变化带来了一系列问题。主要是定子电流和磁链的畸变非常严重,尽管有前面提到的i-n模型,使其表达式中不含rs,不受定子电阻的影响,但它受转子电阻rr、漏电感lσ、主电感l变化的影响。此外还要求准确测量ω,ω的测量误差对i-n模型的影响很大。不过在全速范围内调速应用改进方案即u-n模型还是切实可行的,对此模型前面已有详细说明,不再赘叙。
另外低速时转矩脉动、死区效应、开关频率问题也比较突出。上下桥臂同时导通造成直流侧短路,引入足够大的互锁延时,带来了死区效应。死区效应积累的误差使得逆变器输出电压失真,于是又产生电流失真,加剧脉动和系统运行不稳定的问题。改进方案主要有三个(1)使用改进的开关表,改进控制参数与开关量之间的对应关系,使之产生更优的控制电压波形。(2)以pwm和svm技术实现dtc固定开关频率运行方案。(3)引入模糊控制和智能控制,用软件来解决转矩脉动问题。(4)磁通轨迹改善。采用矢量细分法,消除所选矢量在某些区域的不对称作用而使磁通的轨迹得到改善,并且在磁通旋转速度上也提高了对称性,消除了电流的畸变。
四、直接转矩控制技术发展的展望
随着现代科学技术的不断发展,直接转矩控制技术必将有所突破。现代控制理论和智能控制理论应用于dtc技术,为改进dtc系统提供了坚实的理论依据;同时高性能的数字处理器(dsp)的出现,为改进dtc系统提供了强大的物质基础。尤其是目前数字化潮流势不可挡,各行各业都向数字化靠拢。如智能ipm整合了dsp控制器,将电机控制的大部分电路集成到标准封装的模块中,集成了igbt模块,igbt驱动电路、电压电流反馈、保护模块和dsp控制模块,使得控制结构愈发简单,控制性能与控制精度、响应速度均得到提高。特别是dsp芯片在直接转矩控制系统中的应用为解决低速区的问题提供了可能,因为只要实现了对定子电阻的准确辨识,就能从根本上消除定子电流和磁链畸变,问题也就迎刃而解。而全数字化的实现,将使采样精度更高,误差率更小,更易于实现最优控制。因此利用现代控制理论、人工智能和神经网络理论,将之应用于直接转矩控制技术的研究,从软件着手改进系统将是这种新技术的发展方向。dsp器件的进一步发展也为dtc技术难题突破提供了可能。随着控制性能的不断提高,直接转矩控制在传动领域会有更广阔的应用前景。

