论文关键词:mb-ofdm 正交扩展矩阵 误差权重分布 高阶旋转扩展矩阵
论文摘要:针对mb-ofdm通信系统存在窄带干扰的问题,提出了一种基于高阶旋转扩展矩阵(higher order rotation spreading matrix)的多带ofdm系统。同时用误差权重分布(error weight distribution)方法分析各种角度的高阶旋转扩展矩阵及其他正交扩展矩阵(hadamard, rotated hadamard)的分集度,并在实验仿真中比较了各种扩展矩阵对mb-ofdm系统性能的影响,结果表明各种角度(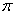 /2除外)的高阶旋转扩展矩阵进一步提高了uwb系统抗窄带干扰的能力。
/2除外)的高阶旋转扩展矩阵进一步提高了uwb系统抗窄带干扰的能力。
1 引言
超宽带(uwb, ultra-wideband)无线通信系统以其高速率、高性能、低功耗、低成本、抗多径、易数字化等诸多优势,已成为短距离无线通信领域中的新亮点,是无线个域网(wpan)的首选方案。超宽带无线通信技术标准有多带正交频分复用(mb-ofdm, multi-band orthogonal frequency-division multiplexing)和直接序列码分多址(ds-cdma, direct sequence code division multiple access)两种技术方案。前者在高速无线数据传输方面具有一定优势,因而获得了越来越多的支持。
uwb系统信道中含有大量的多径能量可供分集接收,在传统超宽带系统中使用卷积编码和比特交织开发信道的分集度,但在高速传输的情况下却不能发挥作用[1]。为了更加有效的提高系统的分集增益,人们把扩展矩阵引入到传统超宽带系统中,如hadamard扩展矩阵[6]。但是文献[8]证实hadamard扩展矩阵不能充分利用多径分量。针对这一问题,本文在mb-ofdm系统中引入高阶旋转扩展矩阵,同时给予误差权重分布的方法分析了各种角度的高阶旋转扩展矩阵及其他的正交扩展矩阵(hadamard, rotated hadamard)的分集度,并用实验仿真的方法比较各种扩展矩阵对mb-ofdm系统性能的影响。仿真结果表明各种角度(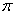 /2除外)的高阶旋转扩展矩阵增强了mb-ofdm系统抗窄带干扰的能力。
/2除外)的高阶旋转扩展矩阵增强了mb-ofdm系统抗窄带干扰的能力。
2 系统描述
根据fcc对uwb信号的定义[1],在mb-ofdm系统中,整个频带(3.1~10.6ghz)被划分成n(14)个带宽为528mhz的子频带,并分为5个频段组,前4个频段组分别由3个子频带组成, 第5个频段组由2个子频带组成。每个子频带使用128个子载波构成一个ofdm子系统,本文为了探究正交扩展矩阵的特性,只使用其中一个子带。系统结构框图如图1所示。
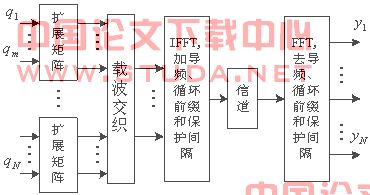
图1系统结构框图
如上图所示,n个子载波被划分为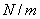 个长度为m的子块,然后用扩展矩阵在这些子块上扩展传输符号,再通过载波交织和ifft之后,传输数据就进入了频率选择性信道。在接收端,fft处理器的输出信号为
个长度为m的子块,然后用扩展矩阵在这些子块上扩展传输符号,再通过载波交织和ifft之后,传输数据就进入了频率选择性信道。在接收端,fft处理器的输出信号为
y=acq+n (1)
a为复正态信道衰落系数的对角矩阵,c为正交扩展矩阵,q是qpsk信号向量,n为零均值复高斯白噪声向量。
扩展矩阵一般用来增加传输符号之间的相关性,和自适应调制不一样,本系统只是利用扩展矩阵而不是重复传输数据来增加子载波数据间的相关性[2],如图2所示
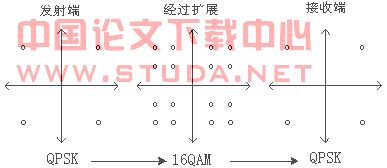
图2经过扩展调制方式的变换过程
在发射端qpsk信号经过正交扩展矩阵转换成高阶调制信号,增加了符号间的相关性,进而提高了整个系统的性能。目前,已有许多正交扩展矩阵可供利用,如hadamard矩阵、rotated hadamard矩阵、低阶旋转矩阵[3][4]等等,本文将着重研究高阶旋转扩展矩阵(维数m>8)及特性。
3 高阶旋转扩展矩阵及特性
文献[2] 提出了一种叫做旋转扩展矩阵的新的正交矩阵,该矩阵比hadamard矩阵、rotated hadamard矩阵跟能提高超宽带系统的性能,其结构形式如下等式
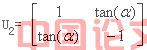 (2)
(2)
旋转扩展矩阵一个很大的优点是选择不同的 ,能灵活的产生多种不同的正交扩展矩阵结构,同时简单的角度旋转就可以比其他的传统扩展矩阵对系统有更好的性能。但是,并不是所有的角度 都能产生性能更好的扩展矩阵,例如 = 时,旋转扩展矩阵依然是hadamard矩阵,当 = 时,qpsk信号经过扩展变换之后还是qpsk映射信号,变换后的调制方式保持不变。下图表示qpsk映射点及角度为 、 和 旋转变换后新的映射点。
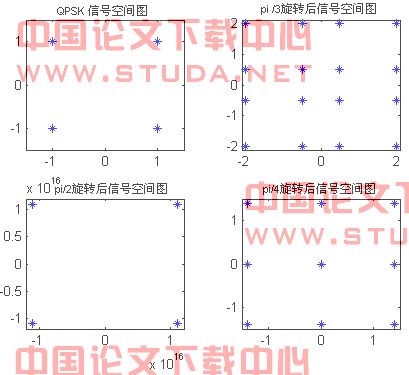
图3 qpsk映射及经过各种角度旋转后的映射方式
我们可以用上面的基本矩阵u2利用ccss[5] (complete complementary sets of sequences)方法构成更高阶的旋转扩展矩阵,其过程可用下面的公式加以描述,

由上面三个公式可以构成m维高阶旋转扩展矩阵,(3)式确保了高阶旋转扩展矩阵保持正交性。基于ccss方法4维旋转扩展矩阵如下所示
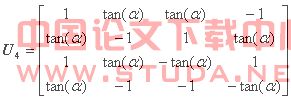 (6)
(6)
对于mb-ofdm系统中的扩展矩阵来说,总是希望它能将信号能量均等地分布在子载波上,这样,即使某一个子载波信道受到严重衰落或干扰,也能从其他子载波恢复原数据。在mb-ofdm系统中,qpsk信号经过扩展操作后传输信号向量为s=cb,所以c的选择决定了信号能量能否等同的分布在向量s上。例如考虑用hadamard矩阵作为扩展矩阵的ofdm系统,如果信号向量b为[1 1 1 1],那么传输向量s为[4 0 0 0],同样的,如果信号向量b为[-1 -1 -1 -1],那么传输向量s为[-4 0 0 0]。从上面可以看出,两个传输向量仅仅在第一个位不同,这样,如果在这个信道有严重衰落就会导致错误的判决。所以好的扩展矩阵应该使传输向量之间的所有位都不同,这里用误差权重来衡量这个特性,误差权重定义为传输向量对不同位的个数,理想上,对于所有的传输向量对误差权重应等于扩展码的维数,才能获得最大的分集增益。表1给出了基于扩展码维数等于4的qpsk调制系统的各种扩展码的误差权重分布。
表1 qpsk调制系统的各种扩展码的误差权重分布
ewd
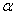 =
=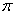 /7
/7
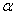 =
=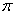 /5
/5
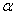 =
=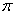 /4
/4
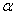 =
=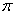 /2
/2
hadamard
rotated
1
0
0
0
192
12
12
2
40
156
198
2270
746
663
3
302
442
1254
4596
1953
1786
4
32181
32042
31188
25580
29929
30179
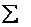
32640
在表1数据中,可以观察出和hadamard、rotated hadamard扩展码相比各种角度的高阶旋转扩展码有很好的误差权重分布特性,大多数的传输向量对所有位都是不同的,但是也有不如hadamard、rotated hadamard扩展码,例如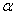 =
=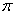 /2的高阶旋转扩展码。
/2的高阶旋转扩展码。
4实验结果与分析
为了分析有好的误差权重分布特性的各种角度的高阶旋转扩展码能否更加有效的提高mb-ofdm的性能,及对抗窄带干扰的有效性,本小节将利用文献[1]提出的信道模型仿真基于各种角度的高阶旋转扩展矩阵及hadamard、rotated hadamard扩展矩阵的mb-ofdm系统,该系统符合ieee 802.15任务组3a提出的标准[1],已在第二小节加以描述。另外,在仿真时假定各种同步是理性的,同时不考虑空子载波和导频子载波。窄带干扰采用多音干扰模型,其可建模为

图4所示的是信噪比为5db、m=64的情况下,mb-ofdm系统的误比特率性能。由图中可以看出,各角度的高阶旋转矩阵(
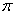
/2除外)比hadamard、rotated hadamard扩展矩阵更能提高系统性能,这和表1中各种码的误差权重分布是一致的,其中角度
/5为的高阶旋转矩阵最大的提高了系统的分集度。
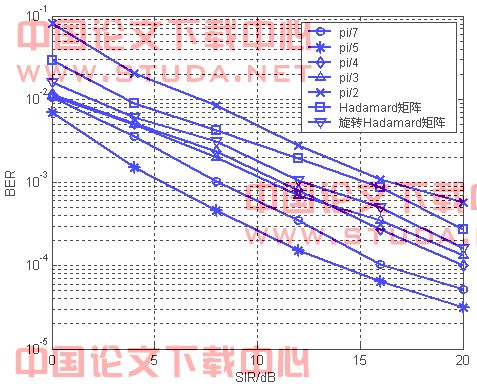
图4 m=64时系统误比特率性能
图5所示的是信噪比为5db、m=32的情况下,mb-ofdm系统的误比特率性能。从图中我们可以观察到,角度为 /7的高阶旋转矩阵比其他角度高阶旋转矩阵及hadamard、rotated hadamard扩展矩阵更好的增强了系统的性能。在文献[3]中m=2的情况下,角度为
/7的高阶旋转矩阵比其他角度高阶旋转矩阵及hadamard、rotated hadamard扩展矩阵更好的增强了系统的性能。在文献[3]中m=2的情况下,角度为 /4的旋转矩阵不能有效的提高系统性能,但在m=32时能很好提高系统的误比特率性能。
/4的旋转矩阵不能有效的提高系统性能,但在m=32时能很好提高系统的误比特率性能。
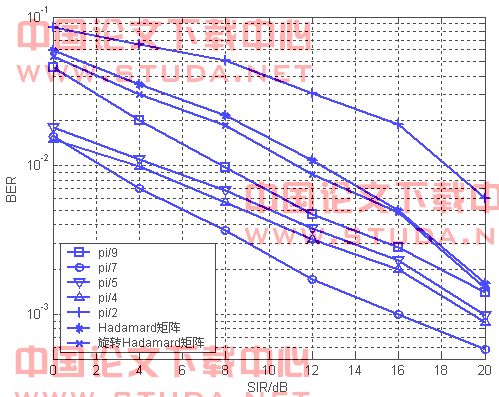
图5 m=32时系统误比特率性能
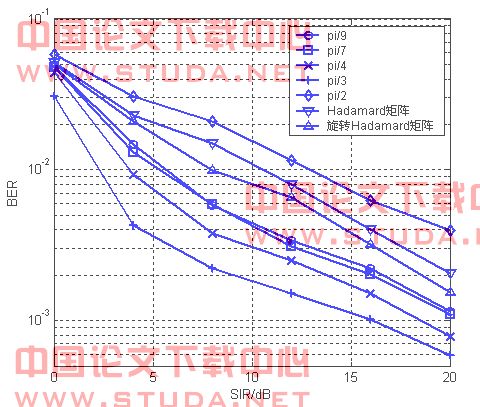
图6 m=16时系统误比特率性能
图6所示的是信噪比为5db、m=16的情况下,mb-ofdm系统的误比特率性能。图中显示角度为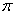 /7的高阶旋转矩阵最好的增强了系统性能。
/7的高阶旋转矩阵最好的增强了系统性能。
5 结论
理论分析与仿真结果表明,各种角度的高阶旋转矩阵利用了mb-ofdm子带部分子载波的频率分集性,增强了系统的性能,同时提高了uwb系统抗窄带干扰的能力。当系统的某些子载波受到干扰或频率选择性衰落影响时,接收机可以从系统的其它子载波中得到传输编码比特的信息。与hadamard、rotated hadamard扩展矩阵相比,好的的高阶旋转矩阵可以降低系统误比特率1个左右数量级。同时仿真结果显示各种扩展矩阵对系统性能的影响与它们的误差权重分布基本符合。
参考文献:
[1] batra a, balakrishnan j. design of a multiband ofdm system for realistic uwb channel environments[j].ieee transactions on microwave theory and techniques,2004,52(9):2123-2138.
[2] ibrahim r,xiaojing huang, raad r. a new spreading matrix for block spread ofdm[c]//10th ieee international conference on communication systems.sinqapore,2006:1-5.
[3] ibrahim r,xiaojing huang,darryn l. a study of different angles for the new spread matrix for bsofdm in uwb channels[c]//the third international conference on wireless and mobile communications.guadeloupe french caribbean ,2007:67-67.
[4] ibrahim r,xiaojing huang, raad r.a study of different angles for higher order rotation spreading matrix for bsofdm in uwb channels[c]//the 2nd international conference on wireless broadband and ultra wideband communications. sydney australia,2007:18-18.
[5] ibrahim r,xiaojing huang, raad r.new higher order rotation spreading matrix for bsofdm[c]//the 2nd international conference on wireless broadband and ultra wideband communications. sydney australia,2007:17-17.
[6] 张士兵,张力军,徐晨. 多带ofdm-uwb 系统的抗干扰研究[j].通信学报,2006,27(5):77-83.
[7] nidhi p,balasubramaniam n,wicom l.impact of error weight distribution in mb-ofdm based uwb system with spreading[c]//2nd international symposium on wireless pervasive computing. san juan,puerto rico,2007:115-119.
[8] bury a,egle j,lindner j.diversity comparison of spreading transforms for multicarrier spread spectrum transmission[j]. ieee transactions on communications,2003,51(5):774-781.

