摘 要 贝叶斯分类能高效地处理大型数据,本文使用核密度估计的朴素贝叶斯分类来进行入侵检测。由于入侵检测审计数据属性多为连续变量,所以在贝叶斯分类算法中使用核密度估计,有助于提高分类的精度,另引入对称不确定 方法 有效地删除不相关的检测属性,进一步提高分类效率。
关键字 贝叶斯;核密度;入侵检测;分类
1 前言
在入侵检测系统中,为了提高系统的性能,包括降低误报率和漏报率,缩短反应时间等,学者们引入了许多方法,如专家系统、神经 网络 、遗传算法和数据挖掘中的聚类,分类等各种算法。例如:cooper & herkovits提出的一种基于贪心算法的贝叶斯信念网络,而provan & singh provan,g.m & singh m和其他学者报告了这种方法的优点。贝叶斯网络说明联合条件概率分布,为机器 学习 提供一种因果关系的图形,能有效的处理某些 问题 ,如诊断:贝叶斯网络能正确的处理不确定和有噪声的问题,这类问题在任何检测任务中都很重要。
然而,在分类算法的比较 研究 发现,一种称作朴素贝叶斯分类的简单贝叶斯算法给人印象更为深刻。尽管朴素贝叶斯的分类器有个很简单的假定,但从现实数据中的实验反复地表明它可以与决定树和神经网络分类算法相媲美
[1]。
在本文中,我们研究朴素贝叶斯分类算法,用来检测入侵审计数据,旨在开发一种更有效的,检验更加准确的算法。
2 贝叶斯分类器
贝叶斯分类是统计学分类方法。它们可以预测类成员关系的可能性,如给定样本属于一个特定类的概率。
朴素贝叶斯分类
[2]假定了一个属性值对给定类的 影响 独立于其它属性的值,这一假定称作类条件独立。
设定数据样本用一个 n 维特征向量x={x
1,x
2,,x
n}表示,分别描述对n 个属性a
1,a
2,,a
n样本的 n 个度量。假定有m个类 c
1,c
2,,c
m 。给定一个未知的数据样本 x(即没有类标号),朴素贝叶斯分类分类法将预测 x 属于具有最高后验概率(条件 x 下)的类,当且仅当
p(ci | x)> p(cj | x),1≤j≤m,j≠i 这样,最大化
p(ci | x)。其中
p(ci | x)最大类c
i 称为最大后验假定,其原理为贝叶斯定理:
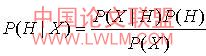
公式(1)
由于
p(x) 对于所有类为常数,只需要
p(x | ci)p(ci)最大即可。并据此对
p(ci| x)最大化。否则,最大化
p(x | ci)p(ci)。如果给定具有许多属性的数据集, 计算
p(x | ci)p(ci)的开销可能非常大。为降低计算
p(x| ci )的开销,可以做类条件独立的朴素假定。给定样本的类标号,假定属性值相互条件独立,即在属性间,不存在依赖关系,这样,
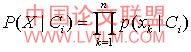
公式(2)
概率
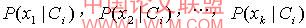
,可以由训练样本估值:
(1) 如果a
k是分类属性,则p(x
k|c
i)=s
ik/s
i其中s
ik是a
k上具有值x
k的类c
i的训练样本数,而s
i是c
i中的训练样本数。
(2) 如果a
k是连续值属性,则通常假定该属性服从高斯分布。因而

公式(3)
其中,给定类c
i的训练样本属性a
k的值,
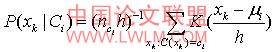
是属性a
k的高斯密度函数,而 分别为平均值和标准差。
朴素贝叶斯分类算法(以下称为nbc)具有最小的出错率。然而,实践中并非如此,这是由于对其 应用 假定(如类条件独立性)的不确定性,以及缺乏可用的概率数据造成的。主要表现为:
①不同的检测属性之间可能存在依赖关系,如protocol_type,src_bytes和dst_bytes三种属性之间总会存在一定的联系;
②当连续值属性分布是多态时,可能产生很明显的问题。在这种情况下,考虑分类问题涉及更加广泛,或者我们在做数据 分析 时应该考虑另一种数据分析。
后一种方法我们将在以下章节详细讨论。
3 朴素贝叶斯的改进:核密度估计
核密度估计是一种普便的朴素贝叶斯方法,主要解决由每个连续值属性设为高斯分布所产生的问题,正如上一节所提到的。在
[3]文中,作者认为连续属性值更多是以核密度估计而不是高斯估计。
朴素贝叶斯核密度估计分类算法(以下称k-nbc)十分类似如nbc,除了在计算连续属性的概率
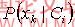
时:nbc是使用高斯密度函数
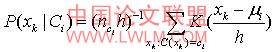
来评估该属性,而k-nbc正如它的名字所说得一样,使用高斯核密度函数来评估属性。它的标准核密度公式为
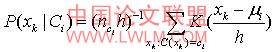
公式(4)
其中h=σ 称为核密度的带宽,k=g(x,0,1) ,定义为非负函数。这样公式(4)变形为公式(5)
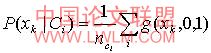
公式(5)
在k-nbc中采用高斯核密度为数据分析,这是因为高斯密度有着更理想的曲线特点。图1说明了实际数据的概率分布更接近高斯核密度曲线。
图1 两种不同的概率密度对事务中数据的评估,其中黑线代表高斯密度,虚线为核估计密度并有两个不同值的带宽朴素贝叶斯算法在计算μ
c和σ
c时,只需要存储观测值
xk的和以及他们的平方和,这对一个正态分布来说是已经足够了。而核密度在训练过程中需要存储每一个连续属性的值(在学习过程中,对名词性属性只需要存储它在样本中的频率值,这一点和朴素贝叶斯算法一样)。而为事例分类时,在计算连续值属性的概率 时,朴素贝叶斯算法只需要评估
g一次,而核密度估计算法需要对每个c类中属性x每一个观察值进行
n次评估,这就增加计算存储空间和时间复杂度,表1中对比了两种方法的时间复杂度和内存需求空间。
4 实验研究与结果分析
本节的目标是评价我们提出核密度评估分类算法对入侵审计数据分类的效果,主要从整体检测率、检测率和误检率上来分析。
表1 在给定n条训练事务和m个检测属性条件下,
nbc和k-nbc的算法复杂度
朴素贝叶斯
核密度
时间
空间
时间
空间
具有
n条事务的训练数据
o(
nm)
o(
m)
o(
nm)
o(
nm)
具有
q条事务的测试数据
o(
qm)
o(
qnm)
4.1 实验建立
在实验中,我们使用nbc与k-nbc进行比较。另观察表1两种算法的复杂度,可得知有效的减少检测属性,可以提高他们的运算速度,同时删除不相关的检测属性还有可以提高分类效率,本文将在下一节详细介绍对称不确定方法
[4]如何对入侵审计数据的预处理。我们也会在实验中进行对比分析。
我们使用weka来进行本次实验。采用 kddcup99
[5]中的数据作为入侵检测分类器的训练样本集和测试样本集,其中每个记录由41个离散或连续的属性(如:持续时间,协议类型等)来描述,并标有其所属的类型(如:正常或具体的攻击类型)。所有数据分类23类,在这里我们把这些类网络行为分为5大类网络行为(normal、dos、u2r、r2l、probe)。
在实验中,由于kddcup99有500多万条记录,为了处理的方便,我们均匀从
kddcup.data.gz 中按照五类网络行为抽取了5万条数据作为训练样本集,并把他们分成5组,每组数据为10000条,其中normal数据占据整组数据中的98.5%,这一点符合真实环境中正常数据远远大于入侵数据的比例。我们首
先检测一组数据中只有同类的入侵的情况,共4组数据(dos中的neptune,proble中的satan,u2r中的buffer_ overflow,r2l中的guess_passwd),再检测一组数据中有各种类型入侵数据的情况。待分类器得到良好的训练后,再从kdd99数据中抽取5组数据作为测试样本,分别代表noraml-dos,normal-probe,normal-u2r,normal-r2l,最后一组为混后型数据,每组数据为1万条。
4.2 数据的预处理
由于朴素贝叶斯有个假定,即假定所有待测属性对给定类的 影响 独立于其他属性的值,然而现实中的数据不总是如此。因此,本文引入对称不确定 理论 来对数据进行预处理,删除数据中不相关的属性。
对称不确定理论是基于信息概念论,首先我们先了解一下信息理论念,属性x的熵为:
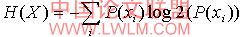
公式(6)
给定一个观察变量y,变量x的熵为:
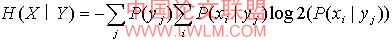
公式(7)
p(xi )是变量x所有值的先验概率,
p(xi|
yi )是给定观察值y,x的后验概率。这些随着x熵的降低反映在条件y下,x额外的信息,我们称之为信息增益,
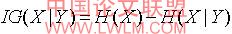
公式(8)
按照这个 方法 ,如果ig(x|y)>ig(x|y),那么属性y比起属性z来,与属性x相关性更强。
定理:对两个随机变量来说,它们之间的信息增益是对称的。即

公式(9)
对测量属性之间相关性的方法来说,对称性是一种比较理想的特性。但是在 计算 有很多值的属性的信息增益时,结果会出现偏差。而且为了确保他们之间可以比较,必须使这些值离散化,同样也会引起偏差。因此我们引入对称不确定性,
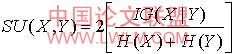
公式(10)
通过以下两个步骤来选择好的属性:
①计算出所有被测属性与class的su值,并把它们按降序方式排列;
②根据设定的阈值删除不相关的属性。
最后决定一个最优阈值δ,这里我们通过 分析 nbc和k-nbc计算结果来取值。
4.3 实验结果及分析
在试验中,以记录正确分类的百分比作为分类效率的评估标准,表2为两种算法的分类效率。
表2 对应相同入侵类型数据进行检测的结果
数据集
算法
dos
(neptune)
proble
(satan)
r2l
( guess_passwd)
u2r
(buffer_overflow)
检测率
误检率
整体检测率
检测率
误检率
整体检测率
检测率
误检率
整体检测率
检测率
误检率
整体检测率
nbc
99.5
0.2
99.79
98.3
0.1
99.84
97.3
0.8
99.2
95
1.8
98.21
k-nbc
99.5
0.2
99.96
98.3
0
99.96
97.3
0.2
99.81
71
0.1
99.76
su+nbc
99.5
0
99.96
98.3
0.1
99.85
98
0.7
99.24
9
1.1
98.84
su+k-nbc
99.5
0
99.96
98.3
0
99.96
98.7
0.2
99.76
85
0.1
99.81
根据表2四组不同类别的入侵检测结果,我们从以下三个方面分析:
(1)整体检测率。k-nbc的整体检测率要比nbc高,这是因为k-nbc在对normal这一类数据的检测率要比nbc高,而normal这一类数据又占整个检测数据集数的95%以上,这也说明了在上一节提到的normal类的数据分布曲线更加接近核密度曲线。
(2)检测率。在对dos和proble这两组数据检测结果,两个算法的检测率都相同,这是因为这两类入侵行为在实现入侵中占绝大部分,而且这一类数据更容易检测,所以两种算法的检测效果比较接近;针对 r2l检测,从表2可以看到,在没有进行数据预处理之前,两者的的检测率相同,但经过数据预处理后的两个算法的检测率都有了提高,而k-nbc的效率比nbc更好点;而对u2r的检测结果,k-nbc就比nbc差一点,经过数据预处理后,k-nbc的检测率有一定的提高,但还是比nbc的效果差一些。
(3)误检率。在dos和proble这两种组数据的误检率相同,在其他两组数据的中,k-nbc的误检率都比nbc的低。
根据表3的结果分析,我们也可以看到的检测结果与表2的分组检测的结果比较类似,并且从综合角度来说,k-nbc检测效果要比nbc的好。在这里,我们也发现,两种算法对r2l和u2l这两类入侵的检测效果要比dos和proble这两类入侵的差。这主要是因为这两类入侵属于入侵行为的稀有类,检测难度也相应加大。在kdd99竞赛中,冠军方法对这两类的检测效果也是最差的。但我们可以看到nbc对这种稀有类的入侵行为检测更为准确一点,这应该是稀有类的分布更接近正态分布。
从上述各方面综合分析,我们可以证明k-nbc作为的入侵检测分类算法的是有其优越性的。
表3 对混合入侵类型数据进行检测的结果
数据集
算法
整体检测
分类检测
normal
dos
proble
r2l
u2r
检测率
误检率
检测率
误检率
检测率
误检率
检测率
误检率
检测率
误检率
检测率
误检率
nbc
98.14
1.8
98.2
0.8
99.8
0
99.8
0
90
0
86.7
1.8
k-nbc
99.78
0.2
99.8
2.3
99.8
0
99.8
0
96
0
73.3
0.1
su+nbc
97.99
2.0
98
0.8
99.8
0
99.8
0
90
0
86.7
1.9
su+k-nbc
99.79
0.2
99.8
1.9
99.8
0
99.8
0
96
0
80
0.1
5 结论
在本文中,我们用高斯核密度函数代替朴素贝叶斯中的高斯函数,建立k-nbc分类器,对入侵行为进行检测,另我们使用对称不确定方法来删除检测数据的中与类不相关的属性,从而进一步改进核密度朴素贝叶斯的分类效率,实验表明,对预处理后的审计数据,再结合k-nbc来检测,可以达到更好的分类效果,具有很好的实用性。同时我们也注意到,由于入侵检测的数据中的入侵行为一般为稀有类,特别是对r2l和u2r这两类数据进行检测时,nbc有着比较理想的结果,所以在下一步工作中,我们看是否能把nbc和k-nbc这两种分类模型和优点联合起来,并利用对称不确定理论来删除检测数据与类相关的属性中的冗余属性,进一步提高入侵检测效率。
参考 文献
[1]langley. p.,iba,w. &thompson,k.
an analysis of bayesian classifiers [a],in “proceedings of the tenth national conference on artificial intelligence” [c] menlo park,1992. 223-228
[2]han j.,kamber m.. 数据挖掘概念与技术[m]. 孟小峰,等译. 北京:机械 工业 出版社. 2005. 196 201
[3]john g.h..
enhancements to the data mining process [d]
. ph.d. the sis,computer science dept.,stanford university,1997
[4]lei yu and huan liu.
feature selection for high- dimensional data:a fast correlation-based filter solution[a],in “proceedings of the twentieth international conference on machine learning (icml 2003)”[c] washington,dc,2003. 856-863
[5]kdd99.kdd99 cup dataset [db/ol]. http://kdd.ics.uci.edu/databases/kddcup99,1999

