论文关键字 :布拉格公式 微波 迈克尔逊干涉
第一章 引言
1913年英国物理学家布拉格父子研究x射线在晶面上的反射时,得到了著名的布拉格公式,奠定了用x射线衍射对晶体结构分析的基础,并荣获了1915年的诺贝尔物理学奖。
衍射现象是所有波的共性,所以微波同样可以产生布拉格衍射。微波的波长较x射线的波长长7个数量级,产生布拉格衍射的“晶格”也比x衍射晶格大7个数量级。通过“放大了的晶体”¾模拟晶体研究微波的布拉格衍射现象,使我们可以更直观地观察布拉格衍射现象,认识波的本质,也可以帮助我们深入理解x射线的晶体衍射理论。
迈克尔逊干涉仪是美国物理学家迈克尔逊和莫雷为进行“以太漂移实验”于 1883年创制的。在光的电磁理论与爱因斯坦相对论形成之前,大多数物理学家相信光波在一种称为“以太”的物质中传播,这种物质充满整个宇宙空间。迈克尔逊和莫雷试图用迈克尔逊干涉仪测量出地球相对于以太的运动。他们预计这种相对运动会导致将仪器旋转90 0 后能观察到4/10个条纹的移动,实际观察到的结果是少于1/100。这个结果令迈克尔逊感到十分失望,但他们因此却创制了一个精密度达四亿份之一米的测长仪器并运用这套仪器转向长度的测量工作。1907年,迈克尔逊由于在“精密光学仪器和用这些仪器进行光谱学的基本量度”的研究工作而荣获诺贝尔物理学奖金。
直到爱因斯坦于 1905年提出了相对论,指出光速不变,即真空中光波相对于所有惯性参考系的速度都是相同的值 c。假想的以太概念被彻底的抛弃。迈克尔逊-莫雷所得的否定结果给相对论以很大的实验支持。它因此被称作历史上最有意义的“否定结果”实验( “ negative-result ” experiment )。
第二章 设计思路 2.1测量微波波长
1. 调微波分光计,使两个喇叭同轴等高,且通过分光计中心,各转至0°与180°。
2. 把固体震荡器接上直流电源,打开电源开关之前为了防止其始电压过大,击穿微波管,应先使电源输出电压旋至最小。打开电源开关后,将电压调至9~10伏。
3.晶体管检波器与微波传播波导管的匹配皆需调节。可用加大衰减的办法,先调节检波器短路活塞的位置,使指示表头达到最大。再调节微波波导管的匹配(方法
同上),使之位置最佳。
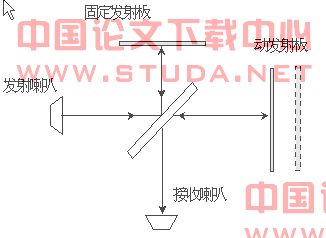 4.测量微波波长
4.测量微波波长
如图b1-5,在分光计上将喇叭(d)旋转90°,并装上动反射镜(m1)和固定反射镜(m2),构成微波迈克尔孙干涉仪。
在小平台上放一玻璃板(p),使之与微波如射方向夹角为45°。只要移动(m1)的位置,就可在检测表头上观察干涉的结果。测定连续3个极小或极大变化之间m1移动距离(相邻两个极小值或极大值时m1位移为1/2波长,并计算出微波波长。重复5次,计算其标准误差。(干涉理论可参见实验s8.3,本教材上册)
2.2验证布拉格公式
1.可用米尺测量模拟晶体的晶格常数d100(本实验用的模拟立方晶体晶格常数d=4cm).
2.将仪器恢复为图b-4状态,适当调节衰减器使表头指针接近满量程,测量立方晶体(100)面衍射一级与二级极大值的掠射角q1与q2。掠射角从20°开始测量,转动两臂每隔1°记录依次表头读数,找出两侧的一级与二级极大值的掠射角,取平均值并与计算值进行比较。
2已知波长测定模拟立方晶体的晶格常数
1.关闭电源休息一下,再启动微波电源继续实验。
2.用(100),(110),(120)晶面族作为散射点阵面,分别测出衍射极大值的掠射角,分别计算d100。(100)面可以利用上面结果。(110)面与(120)面重复实验(二)内容中的步骤2。
2.3数据与计算
记录表格由同学自行设计。
1.利用实验数据计算微波波长,并进行误差分析。
2.验证布拉格公式并求出(100)面晶格常数与实际值d=4cm相比较。
注意事项:
1. 每次开启电源之前,都必须将电源输出电压旋钮旋至最小。
2. 发射器工作电压为9~10伏,工作电压尽可能取得低些,以免发射器过热。过热时停止实验休息以下。
3. 发射喇叭和探测喇叭有增益作用,如果装配不当,信号传输可能被破坏,因此使用过程中不得随意拆下。
第三章 设计方案 3.1实验目的
1、了解与学习微波产生的基本原理以及传播和接收等基本特性。
2、观测模拟晶体的微波布拉格衍射现象。
3.2实验原理
微波波长从1m到0.1mm,其频率范围从300mhz~3000ghz,是无线电波中波长最短的电磁波。
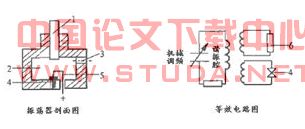 实验装置工作原理:
实验装置工作原理:
图 2体效应振荡器经微波三厘米固态信号电源供电,使得体效应管内的载流子在半导体材料内运动,产生微波,经调谐杆调制到所要产生的频率。产生的微波经过衰减器(可以调节输出功率)由发射喇叭向空间发射(发射信号电矢量的偏振方向垂直于水平面)。微波碰到载物台上的选件,将在空间上重新分布。接收喇叭通过短波导管与放在谐振腔 中的检波二极管连接,可以检测微波在 平面分布,检波二极管将微波转化为电信号,通过a/d转化,由液晶显示器显示。
平面分布,检波二极管将微波转化为电信号,通过a/d转化,由液晶显示器显示。
模拟晶体的布拉格衍射实验
布拉格衍射是用x射线研究微观晶体结构的一种方法。
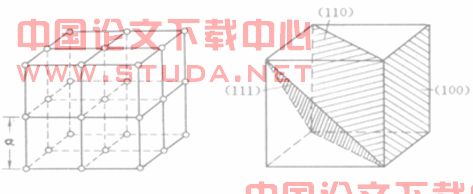
图3 晶体结构
组成晶体的原子可以看作处在晶体的晶面上,而晶体的晶面有许多不同的取向。如图4左方为最简立方点阵,右方表示的就是一般最重要也是最常用的三种晶面。这三种晶面分别为(100)面、(110)面、(111)面,圆括号中的三个数 字称为晶面指数。一般而言,晶面指数为 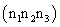 的晶面族,其相邻的两个晶面间距d=
的晶面族,其相邻的两个晶面间距d=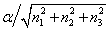 。
。
微波入射到该模拟晶体结构的三维空间点阵时,因为每一个晶面相当于一个镜面,入射微波遵守反射定律,反射角等于入射角,如图5所示。而从间距为d的相邻两个晶面反射的两束波的程差为 ,其中
,其中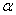 为入射波与晶面的夹角。显然,只是当满足
为入射波与晶面的夹角。显然,只是当满足
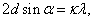
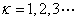 (5)
(5)
时,出现干涉极大。方程(5)称为晶体衍射的布拉格公式。
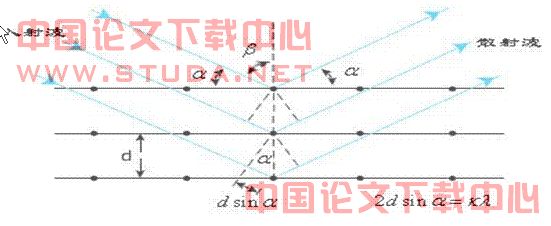
图4 布拉格衍射
如果改用通常使用的入射角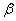 表示,则(5)式为
表示,则(5)式为
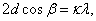
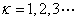 (6)
(6)
3.3实验仪器
dhms-1型微波光学综合实验仪一套,包括:三厘米微波信号源、固态微波震荡器、衰减器、隔离器、发射喇叭、接收喇叭、检波器、检波信号数显器、可旋转载物平台和支架,以及实验用附件(晶体模型、读数机构等)。
3.4实验分析讨论
实验中的误差:本实验的误差主要来自发射喇叭和接收喇叭,通过实验可以明显的看到,当两个喇叭不共线时,实验结会出现较大的偏差。同时由于本实验采用的是3厘米微波,其自身的波长与实验室中的很多仪器设备的限度较为接近,容易发生干涉,衍射,也会干扰微波的测量产生影响。同时由于实验在不对称的环境下进行(一面有强,一面没有),也会对实验产生影响,但是通过近似的实验(在另一侧增加了一块黑板,是两侧近似的对称)发现测量数据并没有太大的变化,由此可知实验环境的对称性对实验没有太大的影响。
第四章 实验结果 4.1 迈克尔逊干涉极小值
(单位:mm)
l1
l2
l3
λi= |l3-l1|
第1次
69.628
52.201
33.671
35.957
第2次
65.401
47.271
30.097
35.304
第3次
64.479
46.623
29.527
34.952
第4次
54.089
35.852
17.752
36.337
第5次
65.702
47.978
30.832
34.870
第6次
53.852
35.861
17.979
35.873
 \* mergeformat
\* mergeformat
35.549
标准偏差:
 \* mergeformat =0.242
\* mergeformat =0.242
4.2 验证布拉格公式
掠射角
20
21
22
23
24
25
26
27
47
48
衍射强度
56
86
95
60
25
4
4
12
2
0
掠射角
49
50
51
52
53
54
55
56
57
58
衍射强度
0
0
0
0
4
10
19
22
30
36
掠射角
59
60
61
62
63
64
65
66
67
68
衍射强度
42
47
52
20
7
4
0
0
0
4

掠射角衍射图
4.3 110晶体验证
已知110一级极大值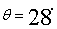 \* mergeformat
\* mergeformat
 \* mergeformat mm
\* mergeformat mm
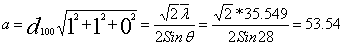 \* mergeformat mm
\* mergeformat mm
结论
通过本次实验我了解了布拉格衍射的原理,对迈克尔孙干涉的测量也了初步的了解。本次实验我学会了一种测量布拉格衍射的方法,对我来说本次实验很成功。由于实验中互相垂直的两块挡板须目测摆放,对结果有一定的影响,但是在允许的误差范围之内。迈克尔孙干涉原理测量微波波长的实验是相当成功的,又试验得出的结果λ=35mm 也非常接近试验仪器的参数。 在实验的过程中,还是总结出如下几条经验:
1 一定要保持晶体中心与载物台中心一致。接受喇叭和发射喇叭要水平正对,下边要水平,保证偏振化方向,保证接受微波强度最强。虽然在实验中仪器有些问题,但还是得到了比较正确的结果。
2 在读数据的时候要统一读最大值或最小值,这样得到的结果比较有效。
3 调节功率时要保证衍射强度最强处微波强度不能超过微安表头的满量程,要保证最大时不超过量程。
4 放上晶体架,架上刻度要与托盘刻度重合,这是我们第一次实验没有注意的,导致数据不准。所以在实验时一定要保证刻度对齐。
5 读数据时最后一位要估读,这是实验中很容易疏漏的。
演示实验是很有趣的实验,在锻炼动手能力的同时,更加锻炼的发现和解决问题的能力,这是作科学研究的基本能力。同时发现只要具有深厚的知识基础才才能将问题研究的更加深入,我们欠缺很多。
参考文献
[1] 王毓银.布拉格验证.北京:高等教育出版社,1992
[2] victor p.nelson.用微机绘制布拉格衍射强度与反射角的关系曲线.北京:清华大学出版社,1997
[3] john m .yarbrough(美).李书浩.布拉格公式.北京:机械工业出版社,2000
[4] 陆坤,奚大顺,李之权.物理面的详解[m].成都:电子科技大学出版社,1997

