空间图形的位置关系是立体几何的重要 内容 ,解决立体几何 问题 的关键在于三定:定性 分析 →定位作图→定量 计算 ,其中定性是定位、定量的基础,而宣则是定位、定性的深化,在面面关系中,二面角是其中的重要概念之一,它的度量归结为平面上角的度量,一般来说,对其平面角的定位是问题解决的先决一步,可是,从以往的教学中发现,学生往往把握不住其定位的基本思路而导致思维混乱,甚至错误地定其位,使问题的解决徒劳无益,本文就是针对这一点,来谈一谈平日教学中体会。
一、 重温二面角的平面角的定义
如图(1),α、β是由ι出发的两个平面,o是ι上任意一点,oc
α,且oc⊥ι;cd β,且od⊥ι。这就是二面角的平面角的环境背景,即∠cod是二面角α—ι—β的平面角,从中不难得到下列特征:
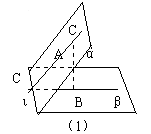
ⅰ、过棱上任意一点,其平面角是唯一的;
ⅱ、其平面角所在平面与其两个半平面均垂直;
另外,如果在oc上任取上一点a,作ab⊥od垂足为b,那么
由特征ⅱ可知ab⊥β.突出ι、oc、od、ab,这便是另一特征;
ⅲ、体现出一完整的垂线定理(或逆定理)的环境背景。
对以上特征进行剖析
由于二面角的平面角是由一点和两条射线构成,所以二面角的平面角的定位可化归为“定点”或“定线(面)”的问题。
特征ⅰ表明,其平面角的定位可先在棱上取一“点”,耐人寻味的是这一点可以随便取,但又总是不随便取定的,它必须与问题背景相互沟通,给计算提供方便。
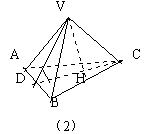
例1 已知正三棱锥v—abc侧棱长为a,高为b,求侧面与底面所成的角的大小。
由于正三棱锥的顶点v在底面abc上的射影h是底面的中心,所以连结ch交ab于o,且oc⊥ab,则∠voc为侧面与底面所成二面角的平面角如图(2)。正因为正三棱锥的特性,解决此问题,可以取ab的中点o为其平面角的顶点,而且使背景突出在面voc上,给进一步定量创造得天独厚的条件。
特征ⅱ指出,如果二面角α—ι—β的棱ι垂直某一平面γ与
α、β的交线,而交线所成的角就是α—ι—β的平面角,如图。
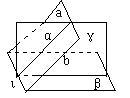
由此可见,二面角的平面角的定位可以考虑找“垂平面”。
例2 矩形abcd,ab=3,bc=4,沿对角线bd把△abd折起,
使点a在平面bcd上的射影a′落在bc上,求二面角a—bc-—c的大小。
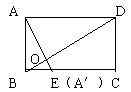
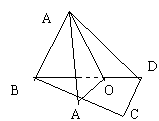
这是一道由平面图形折叠成立体图形的问题,解决问题的关键在
于搞清折叠前后“变”与“不变”。结果在平面图形中过a作ae⊥bd交bd于o、交bc于e,则折叠后oa、oe与bd的垂直关系不变。但oa与oe此时变成相交两线段并确定一平面,此平面必与棱垂直。由特征ⅱ可知,面aoe与面abd、面cbd的交线oa与oe所成的角,即为所求二面角的平面角。另外,a在面bcd上的射影必在oe所在的直线上,又题设射影落在bc上,所以e点就是a′,这样的定位给下面的定量提供了优质服务。事实上,ao=ab·ad/bd=3*4/5=12/5,oa′=oe=bo·tgc∠cbd,而bo=ab2/bd=9/5, tg∠cbd,故oa′=27/20。在rt△aa′o中,∠aa′o=90°所以cos∠aoa′=a′o/ao=9/16,ty∠aoa′=arccos9/16即所求的二面arccos9/16。
通过对例2的定性分析、定位作图和定量计算,特征ⅱ从另一角度告诉我们:要确定二面角的平面角,我们可以把构成二面角的两个半平面“摆平”,然后,在棱上选取一适当的垂线段,即可确定其平面角。“平面图形”与“立体图形”相映生辉,不仅便于定性、定位,更利于定量。
特征ⅲ显示,如果二面角α—ι—β的两个半平面之一,存在垂线段ab,那么过垂足b作ι的垂线交ι于o,连结ao,由三垂线定理可知oa⊥ι;或者由a作ι的垂线交ι于o,连结ob,由三垂线定理逆定理可知ob⊥ι,此时,∠aob就是二面角α—ι—β的平面角,如图。
由此可见,地面角的平面角的定位可以找“垂线段”。
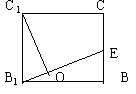

例3 在正方体abcd—a1b1c1d1中,棱长为2,e为bc的中点。求面b1d1e与面积bb1c1c所成的二面角的大小。
例3的环境背景表明,面b1d1e与面bb1c1c构成两个二面角,
由特征ⅱ可知,这两个二面角的大小必定互补,下面,如
果思维由特征ⅲ监控,背景中的线段c1d1会使眼睛一亮,我们只须由c1(或d1)作b1e的垂线交b1e于o,然后连结od1(或oc1),即得面d1be与面cc1b1e所成二面角的平面角∠c1od1,如图,计算可得c1o=4*51/2/5。
在rt△d1c1o中,tg∠c1od=d1c1/c1o=51/2/2。
故所求的二面角角为arctg51/2/2或π-arctg=51/2/2
三、三个特征的关系
以上三个特征提供的思路在解决具体总是时各具特色,其标的是
分别找“点”、“垂面”、“垂线段”。事实上,我们只要找到其中一个,另两个就接踵而来。掌握这种关系对提高解题技能和培养空间想象力非常重要。
1、 融合三个特征对思维的监控,可有效地克服、抑制思维的
消极作用,培养思维的广阔性和批判性。
例3 将棱长为a的正四面体的一个面与棱长为a的正四棱锥的
一个侧面吻合,则吻合后的几何呈现几个面?
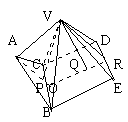
这是一道竞赛题,考生答“7个面”的占99.9%,少数应服从多数吗?
如图,过两个几何体的高线vp、vq的垂足p、q分别作bc的垂线,则垂足重合于o,且o为bc的中点,op延长过a,oq延长交ed于r。由特征ⅲ,∠aor为二面角a—bc—r平面角,结合特征ⅰ、ⅱ,可得vaor为平行四边形,va//be,所以v、a、b、e共面,同理v、a、c、d共面,所以这道题的答案应该是5个面!
2、 三个特征,虽然客观存在,互相联系,但在许多同题中却
表现得含糊而冷漠——三个“标的”均藏而不露,在这种形势下,逼你去作,那么作谁?
由特征ⅲ,有了“垂线段”便可定位。
例4 已知rt△abc的两直角边ac=2,bc=3,p为斜边上一
点,沿cp将此直角三角形折成直二面角a—cp—b,当ab=71/2时,求二面角p—ac—b的大小。
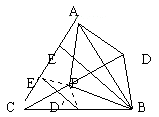
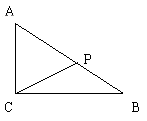
作法一:∵a—cp—b为直角二面角,
∴过b作bd⊥cp交cp的延长线于d,则bd⊥dm apc。
∴过d作de ⊥ac,垂足为e,连be。
∴∠deb为二面角a—cp—b的平面角。
作法二:过p点作pd′⊥pc交bc于d′,则pd′⊥面apc。
∴过d′作d′e′⊥ac,垂足为e′,边pe′,
∴∠d′e′p为二面角p—ac—b的平面角。
再说,定位是为了定理,求角的大小往往要化归到一个三角形中去解,有了“垂线段”就可把它化归为解一个直角三角形。
由此可见,要作,最好考虑作“垂线段”。
综上所述,二面角其平面角的正确而合理的定位,要在正确其定义的基础上,掌握其三个基本特征,并灵活运用它们考察 问题 的环境背景,建立良好的主观心理空间和客观心理空间,以不变应万变。

