论文关键词:知识管理 知识联盟 博弈模型 动态系统
论文摘要:本文在对知识联盟基本性质分析的基础上,构造了一个多阶段博弈模型以描述知识联盟发展过程,证明了该均衡的存在性,分析了均衡存在的条件,并在最后给出了进一步研究的方向。
随着知识资源在企业经营中地位的逐步提高,知识联盟已成为企业获取外部知识的一种重要方式。因此,参与企业获得知识量的大小不仅受到自己付出努力大小的影响,而且受到合作伙伴付出大小的影响。本文通过在寡头竞争环境下分析两个企业参与知识联盟的分析,试图通过分析影响知识转移的主要因素:吸收能力、知识保护力度等描述,得到知识联盟动态发展的博弈过程,为知识联盟的管理提供理论参考。
模型分析
为了分析简便,本文主要考虑寡头竞争环境下,两个寡头企业结成的知识联盟:企业i和企业j。假设该联盟持续了n个阶段(可能是n年或者n个生产周期等),在每个阶段,企业都投入一定的知识资源量
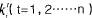
期望通过合作学习积累更多的知识,假设在第h-1(0<h-1≤n)阶段结束时,企业累计的知识投入量
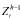
为:

其中,λ表示知识随时间的推移逐步老化而产生的价值折旧率,则企业i在第h阶段获取的知识为:
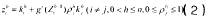
其中,为企业i在第h阶段的吸收能力函数,该吸收能力是指企业识别、模仿、获取并将外部知识转化为商业应用的能力(cohen and levinthal,1989)。由于吸收能力具有很强的累积性和路径依赖性,企业在第h阶段的吸收能力取决于其先前阶段知识的积累量,当=0,即企业i在前h-1阶段没有知识积累,那么企业i的吸收能力为零,越大,企业过去积累的知识量越大,其吸收能力越强,因此吸收能力函数满足下面的假设:

是在第h阶段企业j所贡献知识的透明程度系数,是一个介于0和1之间的变量,知识的透明程度主要取决于企业贡献的知识属性和源企业对知识保护力度的大小。当=0时,表示知识不透明,此时,企业贡献的知识完全隐性,或者说企业对知识的保护力度非常大,企业j没有知识会溢出给企业i;当=1时,表示知识是完全透明的,此时,企业贡献的知识完全显性,或者说企业对知识几乎不做任何保护。参与企业在知识联盟中所贡献的知识不可能完全一样,否则,企业间就没有形成知识联盟的需求和必要,因此,参与企业所贡献的知识属性也不可能完全一样。随着联盟时间的推移,企业对知识保护力度和所贡献知识属性都可能发生变化,所以知识透明程度系数也会随着时间而发生变化。本文将知识透明性作为企业知识联盟发展过程的内生变量,参与企业可以通过控制自己的知识投入量来控制联盟的进展,而且可以有效地改变对知识保护力度或改变所贡献的知识属性来改变知识透明程度,从而控制对方企业对自我知识的吸收。
那么企业i在第h阶段结束时,企业i积累的知识量为:
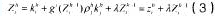
由上式可以看出,企业每个阶段末的知识存量不仅受到企业该阶段自身知识投入量的影响,而且由于知识的溢出和学习,受到其他参与企业该阶段投入的知识量影响。另外,还可以看出,假设企业投入的知识的透明程度恒定的话,企业当期投入的知识量,由于知识溢出性和对手企业的主动性学习,反过来也会提高对手企业的可获知识量。但是,如果企业在每个阶段都减少知识投入量,企业不仅不可以通过自身的知识积累增加知识存量,而且会由于知识积累少,使得吸收外部知识的能力减小,从而减少了从对手企业获得的知识量。因此,联盟中企业能否学习和积累更多的知识,受到联盟中所有参与企业各个阶段投入知识量的大小。
进一步假设,联盟中利益分配的原则是每个参与企业获取利益的大小与其知识投入的大小成比例,因此,企业i获得的利润一般可以用下面的公式表示:
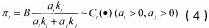
其中,
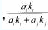
表示市场的销售潜力,表示企业i获得的收益比例,和是企业i和企业j的权重,表示企业每单位投入获得收益能力的大小,表示企业当期的成本函数。一般来讲,不仅受到当期企业i投入知识量的影响,而且与企业i以前的知识积累有关。当期投入的知识量越大,成本越高;企业以前积累的知识越多,其获取新知识的能力越强,即获得单位知识的成本越低。因此满足以下条件:是二级可微(二阶可导,或者,存在二阶导数
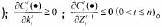
。
为满足上述要求,可以假设成本与当期投入成线性相关,与过去的知识积累成反比例关系,那么该成本函数可以表示为:
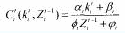
为了进一步推导的方便,在不丢失成本函数基本性质的基础上,可以用一种简单的形式表示该成本函数:
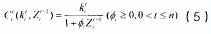
其中,表示过去的知识积累对企业当前学习新知识的影响系数。将公式(3)和(5)代到(4)中可以得出:
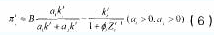
假设参与的企业都是有限理性的,企业联盟的每个阶段开始时,都希望自己这个阶段的付出努力可以在该阶段获得最大的收益。也就是说,企业在第t-1阶段结束时,会以t阶段的收益最大化为目标,根据自身的知识积累和预期的对手企业知识投入量来决定t阶段自己的知识投入量。但是由于对手企业未来阶段的知识投入量是不可能预知的,企业在确定对手下一个阶段知识投入量的时候,可以假设所有企业都认为下个阶段对手企业会延续本阶段的知识投入量(gian-italo bischi,2004),即:=,不失一般性,假设市场的销售潜力为b=1,那么企业i在第t-1阶段结束时,面临的决策问题就是:

在给定企业吸收能力函数和知识透明性程度系数基础上,可以由企业i过去t-1个阶段的知识投入量和企业j过去t-1个阶段的知识投入量推算出来,因此公式(8)给了一个从参与企业过去投入知识量和推算出企业未来每个阶段最优知识投入量的递推公式。假定已知每个参与企业在联盟开始时的知识投入量,那么可以通过(8)式依次推算出以后各个阶段的每个参与企业的最优知识投入量。以两个企业为例,可以得到一个四维的动态控制系统:

根据(9)式和(10)式,可以把两个企业组成的知识联盟的最优知识投入轨迹和参与企业的最优收益轨迹刻画出来,这两个轨迹的描述可以帮助知识联盟参与企业根据各个企业初始知识投入量,进行联盟期间各个阶段知识投入的决策。当然这并不意味着一旦知识联盟企业初始知识投入量确定了以后,参与企业以后各个阶段的最优知识投入量也就确定了,因为知识联盟在实际运作的过程中,参与企业可以通过改变投入知识的类型和属性,增强或减弱对投入知识的保护力度等方法,使得上述的动态系统发生改变,进而改变联盟中每个参与企业的最优知识投入决策。
稳定性分析
通过以上分析可以看出知识联盟的发展是个动态的多阶段博弈过程。在各相关参数给定的条件下,一旦参与企业给定初始投入,可以把这个动态博弈的过程描述出来。但这个博弈过程会不会永远的发展进行下去呢?每个参与企业会不会在联盟发展过程中不停的增加自己的投入以期望获得更高的收益呢?针对这些问题,本文将进一步分析该模型均衡存在的条件并证明存在的可能性。
(10)式实际上是一个四维的非线性迭代方程组,该模型的稳定点一定是在
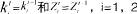
处存在,不失一般性,假设
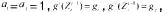
通过对(10)式的变换,可以得到如下的方程组:

为了计算的方便,
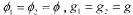
进一步假设,这个假设表示,参与联盟的企业吸收能力、知识保护力度和利用知识的能力都是相等的,也就是说这是两个性质相同的企业参与的知识联盟。通过对上述方程组的数学解析,可知知识联盟稳定点各自的知识付出和知识收益如下所示:

从(11)式可以看出,均衡时参与企业的付出及收益与参数,,都是成正比例的,也就是说,这些参数越大,均衡时企业付出的努力越大,获得的收益越大。
为证明该均衡存在的可能性,求出(10)式的雅可比转换矩阵:此雅可比转换矩阵和的关系到底如何?

其中,
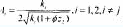
进一步本文求出该雅可比矩阵在均衡点的特征向量: 从
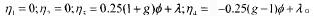
(11)式中均衡存在的条件可以推出,所有的特征值都在大于0小于1,所以,该模型均衡的存在性得证。
结论
本文关于知识联盟动态发展过程的研究是在许多假设的前提下进行的,最后给出的动态控制系统是在各项系数简单化的严格条件下才能适用,虽然如此,该模型还是可以定性地描述知识联盟的动态发展过程,而且证明了模型均衡的存在性,给出了均衡存在的条件,对实际的知识联盟动态发展过程的管理和控制具有一定的指导意义。未来需要深入研究的问题是逐步放松各种假设条件下的知识联盟动态过程的研究,并分析模型中参与企业吸收能力和知识透明性程度这两个因素对联盟动态过程的影响作用,以及现实中企业知识联盟动态发展过程的实证研究。

