摘要：分析并借鉴国外中学数学教材，有利于我国中学数学教材的建设。澳大利亚mathscape教材有两大主要特点：混编安排内容，取材丰富，注重练习的层次性；强调大纲的过程性目标──“数学地工作”。这对目前我国初中数学教材的建设有启示作用：在保持一定系统性和逻辑性的基础上，适当考虑选择性和创新性。
关键词：mathscape教材；数学地工作
澳大利亚包括昆士兰州、维多利亚州、新南威尔士州、南澳、西澳等，基本沿袭了英国的教育体制，除了个别区域（如昆士兰州），基本实行小学6年、中学6年（初中4年，高中2年）的学制，初中教育从7年级到10年级，属于义务教育阶段。澳大利亚mathscape教材是适应目前正在施行的2003年新南威尔士州（new sou-th wales，简称nsw）大纲的系列初中数学教材，共有6本：mathscape7、8、9、10，其中9，10各有两套，分别满足大纲同一阶段不同水平要求的学生，7、8、9正在使用，10即将出版发行并使用。教材的编写者大部分是悉尼大学的数学教师、数学教育研究者①，也有部分中学数学教师参与。
一、新南威尔士州（nsw）数学大纲情况介绍
nsw大纲由州课程研究委员会制定，规定课程的目的是“在数学的应用中发展学生的数学思考、理解，提高能力和自信，培养创造力，以使学生喜欢和欣赏数学，并致力于终生学习”。具体分为知识、技能和理解目标，以及价值和态度目标。大纲充分考虑了不同学生的需求，将整个小学和中学数学学习目标分为6个阶段，阶段1至阶段3是小学1～6年级数学学习的要求，阶段4和阶段5是初中7～10年级数学学习的要求，阶段6是高中11～12年级数学学习的要求。阶段5和阶段6又都分成了不同水平，阶段5包括阶段5.1、5.2、5.3，其中5.3包含了5.2的知识和技能，5.2包含了5.1的知识和技能。阶段6也被分成四级水平：一般性数学、数学、数学扩充1、数学扩充2。上一级水平包含下一级水平。
虽然大纲针对每个阶段安排了内容，但呈现方式却是有弹性的，学生可以学习不同阶段的不同内容，如学生可以学习阶段4有关“数”的内容以及阶段3有关“测量”的内容。不同学生可以达到大纲规定的不同目标，如一个7年级学生可能正在完成小学阶段3的要求，而一个8年级学生，却在学习9年级甚至更高年级的内容。
义务教育阶段大纲对具体内容目标分为“数”“模式和代数”“数据”“测量”“空间和几何”五部分，并提出了过程性目标──数学地工作（work mathematically），要求学生“通过探究、应用问题解决策略，包括选择和运用合适的技术，交流、推理和反思，以发展知识、技能和理解”。
二、mathscape教材特点分析
mathscape教材7、8适应大纲阶段4的要求，9、10适应阶段5的要求，前面提到，教材9、10分别包括两套，一套适应阶段5.2，一套适应阶段5.3（称为mathscape9扩充和mathscape10扩充）。这样，学生在学习教材9（相当于国内初二年级）时就已经有了选择性。教材在内容的编排、材料的选取、练习和习题搭配的层次性，尤其对过程性目标──“数学地工作”的体现上有以下特点。
（一）混编安排内容、取材丰富，注重练习的层次性
教材按照大纲对具体内容目标的分类，以混编方式螺旋式展开。mathscape7的部分内容是回顾和加深小学已有知识，如有关“数”的内容是在小学自然数、分数、小数等基础上进一步研究计数法、罗马数字、斐波那契数字、回文数字、数的平方根和立方根等。其他几册则巩固、发展和进一步扩充前面的相关部分内容，如mathscape8在介绍了mathscape7已有的二维平面的角、几何图形的特点，在三维平面的立体后又研究了平面的毕达哥拉斯定理、角和几何图形、作出几何图形、全等和相似以及圆和圆柱体，mathscape9引进了坐标几何，等等。“数据”部分内容是在mathscape8开始介绍，包括数据表示、数据分析和分类、概率等内容。“测量”内容主要包括时间、长度和周长、面积、体积等的度量。“模式和代数”部分则是在介绍了数字模式和未知数基础上，研究代数式的运算、寻求一般模式并代数化、方程和不等式等的有关内容。每册教材的“数”“模式和代数”“数据”“测量”“空间和几何”五部分内容又划分为不同小节。以mathscape7为例，共分为13章：正整数和数字系统、数字理论、时间、分数、数字模式和变元、小数、整数、代数、角、几何图形的特征、测量和长度以及周长、立体、面积。每章又划分为具体小节（有的达到14节），穿插展开。每册教材内容螺旋式编排，注重与前面内容的衔接。
教材取材丰富，编排生动。每章按照“小节、关注于数学地工作、语言描述有关概念、本章回顾”展开，在部分小节中安排有“试一试”的内容，如“猜一猜我的规则”“一个瓷砖多长”“跑步者”“汽车颜色”等是在“代数式的运算”“毕达哥拉斯定理”“折线图”“解方程”后安排。“语言描述有关概念”是对本章所学主要概念的总结和回顾，以问题形式呈现，要求用自己的语言描述概念，评估对本章内容意义的理解。
教材的练习分成基本练习、巩固练习、进一步应用练习，体现一定层次性。其中巩固练习是最主要的部分，题量较大，有时达20多个，不过一般学生都能够完成。进一步应用是难度相对提高的练习，其问题可能是开放性的，也可能包括扩展材料或大纲外的材料，但大部分问题仍然是一般学生能够接受的。三部分练习题目的难易程度有明显区分。
（二）强调大纲的过程性目标──“数学地工作”
教材在每章具体内容的后面安排有“数学地工作”，以强调大纲对此部分的要求，这是本套教材的最突出特色。教材从现实生活引入，然后是数学问题，按照“引入、学习活动、挑战、交流、反思”进行，以加深对本章知识的理解。此部分选材尤为丰富，从古到今、从人文地理到社会、从数学到其他科学等，通过丰富和有创意的联系生活实际的素材，体现了数学知识的综合应用和相互联系，如“澳大利亚的本土居民”“神秘社会”“数学和魔法”“网球锦标赛”“一个核潜艇的相对尺寸”“梦、想象和数学想法”“分裂原子”等。下面介绍的是mathscape9“代数”一章“数学地工作”的实例，是在介绍完模式与代数以及代数式的运算等内容后安排的，体现了通过学生的探究、解决问题过程，以加深对知识的理解，并培养交流、推理和反思等能力的过程性目标的要求。
数学地工作──“来自于帕斯卡1654年的数字模式”
引入：
帕斯卡（blaisz pascal 1623—1662），法国伟大的数学家、哲学家、作家和神学家，是与费马（fer-mat）和笛卡儿（descarte）同时代的人。尽管他在几何上做了很多贡献，人们记住更多的仍是帕斯卡三角形：
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
……
其中每个数字是它上面一行相邻两个数字的和。这早就为人们所知。然而帕斯卡是第一个系统地探究其模式的人，而且得到了（a＋b）n（n是正整数）的代数展开式的字母系数，如（a＋b）2＝1a2＋2ab＋1b2。
假定三角形最上端的顶点1作为第0行，则“1 2 1”是第2行，我们的活动就从这儿开始。
学习活动：
1．第10行的数字应该是什么？
2．写出n＝0，1，2，3，4，5时的（a＋b）n的展开式，并完成下表：
n
展开式
0
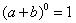
1
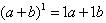
2
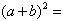
3
4
5
3．当展开式中b的指数增加时，a的指数有什么变化特点？运用模式预测：
（a)（a＋b）6的第一个和最后一个字母；
（b）第二个字母；
（c）第四个字母。
4．写出（a＋b）6和（a＋b）10的展开式。
5．取b＝3，猜测（a＋3）5的展开式。
6．假定最上面的数字1作为第0行，将每一行的数字相加，有什么规律吗？第n行的数字和是多少？
7．将每一行作为一个独立数字，如1，11，121，1 331，14 641，…，你注意到了什么？
8．你能否发现1，3，6，10，15，…以及斐波那契数字？你还能发现哪些数字模式？
挑战：
1．在当地冰激凌店中有19种口味供你选择，你想一次买三种口味品尝，可以得出供你选择的不同方式共有1 330种。提示：三种口味都相同，三种口味都不同，两种口味相同而另一种不同。
注意：两个草莓口味和一个香草口味的冰激凌，与一个香草口味和两个草莓口味的冰激凌是同一个选择。
2．解释和说明下面表格中的数据
冰激凌的品种数（n）
可供选择的总数目
（每次选三个品种）
1
1
2
4
3
10
4
20
3．继续完成上表，当n＝19时，你是得到1 330种选择吗？
4．在帕斯卡三角形中你能否得到数字模式：1，4，10，20，…？
5．对此问题有个一般性解答，如果有n个品种，那么会有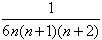
种选择，验证n＝1，2，3，4成立，并示n＝19时的值。
交流:
分组活动，完成下面两个表格并展示你的结果。
1．制作一个表格，描述（a＋b）n的展开式（称为二项式定理）和帕斯卡三角形的关系，说明如何不通过具体相乘而写下展开式的字母，可以包括a＝b＝1的特殊情况。
2．制作一个表格描述帕斯卡三角形中你能找到的不同数字模式。
反思：
帕斯卡崇尚“直觉”，一种不需要借助推理的能力。在他的数学工作中他喜欢预测结果，他经常表现出极好的猜想和发现捷径的能力。
你喜欢对一个问题作出猜想和寻求捷径吗？帕斯卡的一个著名结论是：“推理是那些不知道事实的人发现的慢和曲折的方法。”你赞同这个观点吗？反思“直觉”在数学学习中的作用，并和你的老师讨论一下。
三、从mathscape教材分析和思考中国初中数学教材
mathscape教材在一定程度上体现了澳大利亚nsw初中数学教材的特点，对照中国初中数学教材，并结合中国国情，笔者提出以下思考和建议。
（一）如何对待选择性和统一性
澳大利亚大纲从阶段5就有了选择性，同一年级学生允许达到不同的水平和要求，有为优秀学生准备的专门教材，如mathscape9扩充和mathscape10扩充，也允许学生进行较低阶段水平的学习，如8年级学生可以学习7年级的课程等。学生初中毕业后有两种选择：继续学习两年的高中课程后升入大学或选择直接工作，这体现了学生数学学习的个性差异，反映了教育不能以相同模子塑造人才的特点。对此，我们要结合社会背景进行分析。
首先，要分析国情。澳大利亚大学入学没有年龄限制，大学入学率相对较高，学生初中毕业后可以选择先工作，有一定实践经验后再进入大学学习。澳大利亚的大学教育也充分考虑了学生的个性差异，达到不同阶段要求的学生升入大学后，可以选择学习大学数学的不同水平。
其次，要分析学生的实际情况。在低年龄段就实现数学学习的分流，有可能会使部分学生仅仅因为某些暂时困难，或个人的兴趣和爱好就放弃数学学习，而必要的某些数学训练对一个人适应社会还是非常重要的。
因此，中国初中数学教材在选择时，就需要充分考虑我国的国情、考虑中学教育与大学教育的衔接以及可施行性与渐进性等。以往的初中教材较多关注了学生的整齐划一，要求学生按照同一步调达到相同水平，实际这是很困难的，因为不同学生的数学学习速度、学习水平是不一样的，目前阶段，考虑针对同一内容的不同水平要求，或对优秀学生的学习内容补充或提前进行下阶段的学习等，是较为现实可取的。
（二）如何看待基础性和创新性
mathscape教材按照“数”“模式和代数”“数据”“测量”“空间和几何”五部分混编、穿插安排内容的方式，可以使学生体会代数、几何、统计等内容的相互关联，但过分零散而又较为独立的分章节安排，又很难让学生体会数学知识的整体性和系统性，难以从众多的各小节中理清本章以及整本教材中这五部分内部的线索，也没有一个严密的逻辑体系贯穿其中。中国初中数学教材需要体现知识之间的关联，体会代数、几何、三角、统计等内容之间的联系，这是我们以前较为忽视的，但同时，我们不应该放弃我们的优势所在：注重数学知识的系统性和逻辑性，注重基础知识和基本技能，培养良好的思维习惯等。
mathscape教材的一大特点是内容取材丰富，从古代玛雅文化到现代核潜艇，从分裂原子到太阳系，从悉尼的市场价格到世界健康问题，内容包罗万象，教材厚度合适（32k本 500多页），既是一本教科书，一定程度上又是一本内容丰富的课外读物；既有数学的概念、定理，又有这些概念、定理的实际生活应用背景，包括某些挑战性题目练习等。从上面所举“数学地工作”的实例中，我们不难分析看出如下训练：1．通过对历史人物帕斯卡的介绍，扩大学生的知识面，提高数学学习的兴趣。2．重视对学生进行猜想、归纳、发现等合情推理能力的培养，如通过观察数字特征，寻找代数展开式的规律，发现代数展开式的字母系数与帕斯卡三角中数字之间的关系，以及探究帕斯卡三角形数字的其他规律，等等，使学生经历帕斯卡最初发现的过程。3．随后的选择不同品种的冰激淋问题，实际是将有关组合、规律探究，以及代数式和帕斯卡三角形数等融合在一起的问题，也是一个现代问题和古代问题相结合的问题。4．通过分组活动并展示结果，以及反思数学中的直觉，使学生进一步理清所经历的发现过程以及发现的结果，评判自己的思维过程，进而培养批判性思维品质。mathscape教材的这一特点促使我们思考：如何让我们的教材体现创新性，培养学生的交流能力、反思能力和创造能力等。对此，考虑的几种可能实现途径有：展现知识的发现过程，以使学生经历猜想、发现、归纳等过程；丰富内容素材、提供来于生活实际和数学内部的问题，以及更多挑战性问题；指导利用教材以外的更宽泛学习资源，如互联网、数学杂志、课外读物等，充分发挥学生潜能；引导利用各种可能的其他学习途径，如小组学习、综合活动、实践调查、小组或个人报告等，促进数学学习兴趣，培养创新能力。
另外，mathscape教材通过数学知识的具体应用进一步体现数学概念和定理的意义，还通过教材配套光盘介绍大纲本阶段的目标。这也是可以吸取之处。
总之，中国初中数学教材可以在保持一定系统性和逻辑性的基础上，适当考虑选择性和创新性。我们以往教材重视系统性，这是我们的特色。如何使得这一特色更加符合学生的认识规律和认识特点，符合社会发展特点，是应该我们深入研究的。国外教材的选择性、开放性、创造性是需要我们学习和借鉴的，然而，过分零散、缺乏系统和逻辑的编排体系是否适合中国的中学数学教学，如同上面实例介绍的，我们也可以反思一下，“如何理解教材中的推理，教材对培养推理和直觉的作用”等。目前中国初中数学教材的系统性和逻辑性是需要的，是需要一种适度的、符合学生特点的系统性和逻辑性。同时，我们也要认识到，我们的教材是面向有生机、有活力的生机勃勃的青少年，他们需要继承前人的知识，也需要创新，他们喜欢挑战，也需要挑战，只有让我们的教材在保持已有优良传统的基础上，进一步增加教材的挑战性、亲和性、时代性，才是学生喜欢并乐于接受的教材。
①澳大利亚悉尼大学隶属于新南威尔士州。
