论文关键词：不完全信息  博弈论  药 品 市场   交易机制

　　论文摘要：针对政府集中招标采购基础药品的情况，在制药厂商生产 成本 或生产函数为私人信息的前提下，应用博弈论中关于暗标拍卖理论及机制设计理论，试图通过建立政府基础药品采购的最优拍卖机制的博弈模型，得到竞标的最优交易机制，继而为政府价格监管部门对药品市场的信息引导提供理论的依据和政策支持。

　　任何市场都不存在完全的信息，没有任何一个市场的信息是完美的，市场中的成员或多或少的拥有私人信息。那么 ，在不完美信息的市场上，用概率模拟估计的方法就为实证性研究不完全信息条件下招投标策略提供了有益的参考。但这种方法实质上是将不确定性信息问题转变为确定性信息问题，从而掩盖了因不完全信息带来的逆向选择(advf2rse selection)和 道德 风险(moral risk)。在我国，制药厂家繁多，市场供应量大，生产成本和产品质量参差不齐，竞价机制 尚不完善 的情况下 ，药品市场 上就普遍存在逆 向选择 和道 德风险。作为这二者的 数学 描述，激励约束机制是不完全信息问题的研究重点。本 文以政 府的集中采购基础药为例，通过对不完全信息条件下 同类药品制造厂商 的竞价行为分析，推导出药品的采 购的激励约束交易机制 ，从价格监管的角度 ，得出同类药品的政府采购最优拍卖机制。

　　一、基本概念和理论准备

　　(一 )类型

　　类型是指一个市场成员或局中人在某个时间点上所具有的初始私人信息，每个局中人的类型集都是实数轴上的一个区间，每个局中人 的效用对于他 自己的类型都是线性且相互独立的，它是不完全信息门表现。本文以同类药品生产商的生产成本或生产函数为各自的类型；生产商 i的类型集用  表示，其中的元紊用 t 表示，t— 表示类型集中除ti外的其他元素。在以下的分析中假定局中人类型的概率分布是它们之间的共同知识。

　　(二)贝叶斯博弈的显示原理

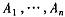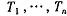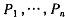　　所谓贝叶斯条件是指，在非完全信息状态下，局中人的行动空间，其类型空间，判断值及他们的收益函数；其中局中人 的类型作为局中人i的私人信息，是单位商品对他的货币价值，它决定了局中人 i的收益函数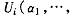 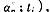并且是可能的类型集  中的一个元素。局中人 i的判断 p；描述了 i在给定自己的类型是t 时，对其它 n—1个局中人可能的类型 t— 的不确定性。我们用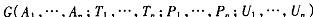来表示这一博弈。 贝叶斯博弈的显示性原理表明 ，局中人相互之间通过一个调解人 通信 ，调解人首先要求每个局中人 向它透露全部私人信息，然后它向每个局中人只透露引导其行动的必要的少量信息。按照这种方式，没有一个局中人会有报谎或不服从的动机。贝叶斯博弈的显示性原理是研究不完全信息的一个最重要原理，它为市场 管理 者或规划者进行机制选择提供了理论基础。

　　(三)激励相容的交易机制

　　一个交易机制 at用一个偶对(q，y)来表示，使得对于  中任意t都存在 (q，y)(t)=(q(t)，y(t))=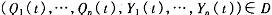 (其 中 d为 社会 的选择对象集)。q表示成交的商品数量，y表示成交时的净货币支付，二者都是局中人类型组合 t的函数。一个激励相容机制是指满足以下信息激励约束的机制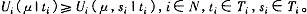：式中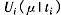：表示在交易机制  下 ，当局中人 i的类型为 t 时的收益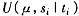；表示当局中人 ￡的真实类型为 t 而谎报为s 时所获得的收益。激励相容机制表明，没有人可以从这个机制中通过谎报而增加收益。

　　二 、基本假设和模型的构建

　　对于药品市场的价格监管部门，虽然有权要求各个制药厂向其提供成本 材料 ，但这种成本都是各个制药厂的事后成本或 历史 成本，因此无法掌握各个制药厂在竞价过程中的实际动态成本，而只能从各个制药厂商的事后成本，估计整个动态成本的变动范围以及在这个范围内的分布概率。因此，在监管部门与厂商之间就存在着不完全信息的问题。在基础药品政府集中采购的过程中，基本是按竞价的模式进行。在这种信息不完全的竞价情况下，在保证同类药品同质的前提条件下，采购费用的最小化机制就是所要求的激励相容的机制，既集中采购的最优拍卖机制。下面将按照具有线性效用的贝叶斯博弈理论展开对模型的推导。

　　假设在 市场 上存在 17,个生产同类 药 品的制药厂既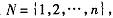，市场上该药品的总需求为 q，且每个制药厂 i所具有的一个类型是给定两个参数l(i)和m(i)和之间的一个实数，所以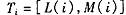对于每个 i，令  是区间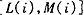上一个正的连续概率密度函数，并且假设每个另外的制药厂．都认为制药厂i的类型是具有概率密度  的一个随机变量，且独立于所有其余局中人的类型。以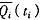表示当制药厂 的类型为 t 时，该制药厂在市场上的成交量期望值； (t )表示当制药厂 i的类型为t 时，该制药厂所获得收入的 期 望 值。则 有：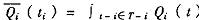

　　

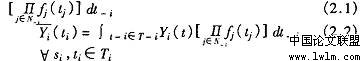
　　式中 t表示其余制药厂的类型，显然存在 t=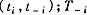为其余制药厂的类型集。 如果制药厂 i在竞价过程中诚实的报告其投标时的类型，则制药厂 i期望净收益为 ：

　　

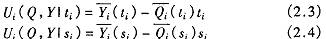
　　如果制药厂 i在报告其投标类型时谎报，即它的真实类型是 t 时而报告为s ，或当真实类型是 s。时报告为ti，但其他制药厂仍然遵守诚实报告其类型的战略则制药厂 i的期望收益为 ：

　　

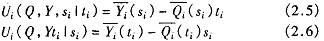
　　要使(p，y)为一个激励相容机制 ，则必须满足以下信息激励约束 ：

　　

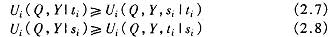
　　将式(2．3)～(2．6)代人式(2．7)和(2．8)中，得到下式 ：

　　

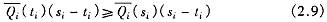
　　以上说明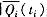是 t 的非减(从而也是黎曼可积①的)函数 ，并且有： 　　

　　

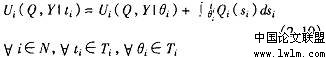
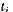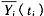　　于是 ，在局中人 i的类型。被决定前的期望值是

　　

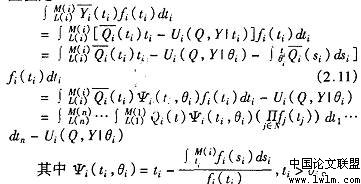
　　其中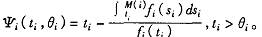

　　再令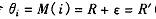 (其中 尺为边际报价e为任意大于零的数)，所以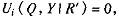于是有竞标采购费用的期望值：

　　 

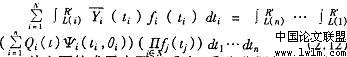
　　从上面的式子中可以看出，采购费用仅仅取决于q函数，而 q函数又是描述每个制 药 厂成功取得标底的概率是如何依赖各制药厂(报告的)类型的函数，同时注意到，一个等价的激励相容机制总是一个将拍卖品交付给对该物品有着最高真实评价的局中人的机制，因此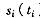，可通过采购的竞标模型来确定。那么政府集中采购的竞标模型可以表述为：

　　

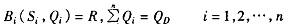
　　上式中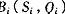表示制药厂的报价函数，s 为制药厂i的报价策略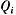，为该厂商的产量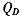，  为整个 市场 上此类药品的总需求量。现在我们要找到使政府效用最大化的激励机制，它同时也满足各个制药厂商产量达到市场需求条件下的 社会 受益的最大化。具体公式表述如下：

　　

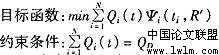
　　因此，在竞价过程中，假定制药厂 i的真实类型(即其 成本 )为￡ 他的投标价格为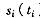。根据贝叶斯博弈的显示原理，这个激励相容的最优拍卖机制不但使的购买费用达到了最小，而且能保证总是优先交付给提供真实生产成本(即其类型 t )的厂商，从而保证了市场的公平性和有效性 。所 以价格监管部门应加强投标市场的信息 管理 与信息发布，以引导各诚实投标，并由自身的拍卖达到一种最优的状态。这种拍卖机制就是在不完全信息条件下同类药品制药厂的交易机制。

　　三、结论

　　在政府集中招投标采购基础药品的模式下，单一购买者承担了药品市场全部的买方风险。由于客观上存在各制药厂商与政府价格监管部门之间的信息不完全，价格监管部门面临一个需要解决的问题就是如何促使各制药厂商诚实地参与投标 ，并同时使集 中采购的费用支出最低。本文根据贝叶斯博弈的显示性原理 ，推导了在这种信息不完全的条件下，政府集中采购基础药品的最优拍卖机制。在这个交易机制中，没有一个制药厂商可以通过谎报来增加收益，并同时保证了政府集中采购的成本费用最低。政府的价格监管部门应通过加强药品招投标市场的信息管理与信息发布来实现这种投标机制。

　　参考文献：

　　[1]谢识予． 经济 博弈论[m]．上海：复旦大学出版社，2002．

　　[2]黄涛．博弈论教程[m]．北京：首都经济贸易大学出版社2004．

　　[3]吴任吴．博弈论与信息：博弈论概论(第二版)[m]．北京北京大学出版社。2004．

　　[4](美)罗伯特．吉本斯，高峰译．博弈论基础[m]．北京：中国社会科学出版社，1999．

　　[5](美)潘卡基．格玛沃特，胡汉辉、周治翰译．产业竞争博弈[m]．北京：人民邮电出版社。2002．

　　[6](美)佛登伯格，(法)梯诺尔著，黄涛、郭凯等译．博弈论[m]．北京：中国人民大学出版社 ，2002．

　　[7](法)泰勒尔著，张维迎总校译，《产业组织理论[m]．北京中国人民大学出版社，1998．

　　[8]kyle bagwell and asher wolinsky。game theory and industriaorganization，in：hal皿iook ofcame tlaeory th econornic ap—plications，2002．

　　[9l erie rasmusen，games and information，fourth edition， basil bla&we]l publishing，nov 2006．

　　[10]martin j．oslmme&ariel runnsteln，a c0ui in canle the0．ry，the mitpress，1998．