摘 要:应用自回归条件异方差(arch)模型对上海股市在2007年4月27日至2008年4月28日股指日对数收益率进行建模分析:结果反映沪市股指收益率具有明显的波动聚集性和尖峰厚尾的特征;均值模型适合arma过程,且不符合股市弱有效的特征,回归模型具备预测能力;无条件期望收益率不受到当期风险的影响;条件方差具有明显的非对称性和杠杆效应。
关键词:条件异方差;股市弱有效;非对称性;波动率
1 引言
股票市场价格的波动性主要体现在未来价格偏离期望值的可能性,其中对期望价格的偏离有价格上涨的上偏离和价格下跌的负偏离。股票的波动性代表了其未来价格的不确定性,这种不确定性一般用收益率的方差或标准差来刻画。
股票波动率的一个特殊性是它不能被直接观测,尽管如此,波动率的一些特征往往是在资产收益率序列中能看到。首先,存在波动率聚类。第二,波动率以连续方式随时间变化,即波动率跳跃是很少见的。第三,实证结果呈现收益的经验分布显著不同于独立正态同分布,表现为尖峰厚尾特征。第四,波动率不发散到无穷,即波动率是在固定的范围内变化。从统计角度说,这意味着波动率往往是平稳的。第五,波动率对价格的大幅上升和价格大幅下降的反应不同,称为“杠杆效应”。
2 数据描述
构造收益率序列的方法是对股票市场价格取对数,然后做一次差分。
2.1 收益率{r
t}的正态分布检验
{r
t}序列的261个观察值的均值为0.000253,样本方差为0.024452。收益率序列的偏度为-0.5015——呈现负偏态,有一个较长的左尾,即出现极端正收益率的概率要大于出现极端负收益率的可能性。峰度大于3——呈现尖峰厚尾,表明收益率出现异常值的概率要大于正态分布时的概率。jb统计量的先验概率为0%,拒绝原假设:序列满足正态分布。不满足正态分布、呈现尖峰厚尾,初步表明:序列可能存在异常值成群出现的现象。
2.2 收益率{r
t}的平稳性检验
序列{r
t}在水平值下进行单位根检验,adf值为-15.67,而在1%的水平下临界值为-3.46,所以在1%的显著性水平下拒绝原假设:存在单位根,即{r
t}序列是平稳的。
2.3 收益率{r
t}的序列相关性、独立性检验
计算分析知,自相关系数滞后3阶时,显著不为0,q(3)、q(4)在5%显著性水平下显著异于0,拒绝
1=
2=
3=0的原假设,认为其中至少有一个显著为0,显示前后收益率存在相关性。可以考虑拟合ar(3)、ma(3)、arma(3,3)模型。同时可以认为沪市在2007年4月27日至2008年4月28日期间不符合股市弱有效的特征,回归模型具备预测能力。
通过对系数显著性(显著)、拟合优度、残差平方和、aic,sc(越小越好)的检验,认为arma(3,3)的结果最优。
r
t=-0.7r
t-1-0.98r
t-2-0.61r
t-3+ a
t +0.74a
t-1+0.97a
t-2+0.75a
t-3
进一步检验收益率序列的平方的相关性特征,注意到{r
t2}序列的自相关、偏自相关系数发生微妙的变化。部分{r
t2}序列的acf系数比原序列的有所增大,并且呈现出一定的规律性,不像原序列显著为零。与此同时,q统计量拒绝相关性的概率也在减小,原序列滞后1阶时,拒绝相关性的概率达到72%,而{r
t2}序列拒绝原假设的概率仅达到43%,这说明收益率{r
t}序列前后期不独立。
这种序列有弱相关性但却不独立的特征,进一步说明,收益率{r
t}序列可能存在arch效应。
2.4 收益率{r
t}的arch检验
对arma(3,3)模型的残差做arch-lm检验,滞后=5时,检验的相伴概率p=0,arch-lm检验拒绝不存在arch效应的原假设,说明上证收益率存在arch效应(与之前的正态性检验结果一致)。
通过对收益率序列的描述:呈现尖峰厚尾特征,序列平稳,前后相关性弱,但不独立,所以采用arch类模型拟合收益率序列。
3 模型的遴选
根据均值方程的残差序列的正态检验结果,得出残差序列不服从正态分布,有尖峰厚尾现象——因此选择残差服从t分布。
拟合arch族模型,其中包括arch-m模型和非对称模型。
数据显示以下特点:(1)实证结果显示风险溢价参数(ρ)并不显著,即收益率与过去的波动率无关,所以arch均值模型不适合。(2)杠杆效应显著,应拟合非对称模型。(3)均值模型中常数项显著为0。(4)tarch模型系数应满足大于零条件,保证均值修正后的收益率的无条件方差有限,但估计方程的系数没有满足这个条件,所以tarch模型不适合。
数据特征将我们的注意力引向egarch模型,arma(3,3)-egarch模型的均值方程中除了ar(3)的系数显著不为零外,其余系数都不显著。基于精简准则和aic、sc最小化准则选择合适的模型,最终的选择是arma(3,3)-egarch(0,1)模型。

进一步探讨,对一个arch族模型,标准化残差是服从标准正态或标准t分布的随机变量,可以通过检查标准化残差来验证拟合模型是否合适。实证结果表明标准化残差具有几个特点:(1)自相关系数不显著,q统计量先验概率基本大于50%,可以得结论:标准化残差不相关。(2)标准化残差平方值序列不相关。(3)杠杆效应显著。
4 结论分析与评价
文中应用自回归条件异方差模型对沪市在2007年4月27日至2008年4月28日股指收益率进行建模分析,结果反映沪市综指日对数收益率具有以下特征:
4.1 解释均值模型
(1)日对数收益率的无条件期望收益率为零,即长期均衡水平为零。
(2)当期的日对数收益率均值受到t-3期收益率的影响,且影响能力较强(影响系数接近1),但不受到t-1,t-2期收益率的影响,说明市场中有“等待效应”,等待期限为3个工作日,这可能与大部分短信交易往往要有确认信号出现有关。
除此之外,t期日对数收益率均值还受到前3期抖动的影响。
4.2 解释方差模型
(1)收益率波动性受到前期标准化抖动和前期波动性的影响。
(2)
1+
1的大小决定了外部冲击对未来时刻的波动率产生影响的持续性,称为衰减系数。
1+
1=0.62,衰减系数较小,外部冲击的衰减速度较快,(0.62)5=0.09,表明t时刻的波动冲击在t+5时刻,仅残留9%。
4.3 解释非对称性及杠杆效应
(1)≠0说明冲击的影响存在非对称性,<0说明沪市的非对称信息效应体现为显著的收益负冲击效应,即“利空”消息对股市的影响大于“利好”消息对股市的影响。
(2)
1+的值为负,前期波动率给定,前期抖动减少一个单位(形成负抖动,利空消息)会使条件方差的对数值增加0.08个单位,前期抖动增加一个单位(正抖动,利好消息)实际上会使条件波动降低0.52个单位,说明“好消息”会降低条件波动。
对波动率方程做一个反对数变换,研究表明变动一个单位标准差的负抖动对波动率的影响要比相同强度的正抖动的影响要高55.3%。
(3)<0说明杠杆效应存在,杠杆效应可以理解为当前收益和未来波动之间很强的负相关,收益增加时波动减小,收益减小时波动增加。
(4)绘制非对称信息冲击曲线能从图形上直观的表明“利空消息”和“利好消息”对波动的影响:曲线在信息冲击小于0时,代表负冲击,负冲击会增加条件波动,正冲击会减小条件波动。
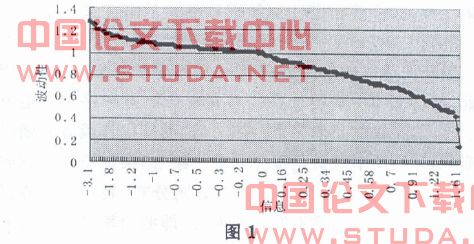
4.4 解释收益率与风险的相关性
拟合arch族模型过程中,注意到资产预期收益与预期风险不相关,风险溢价参数显著为0,说明沪市日对数收益率与波动率无关,排除风险溢价的存在是收益率前后弱相关的原因。
参考文献
[1]张雪莹,金德环. 金融计量学教程[m].上海:上海财经大学出版社,2005.
[2]高铁梅.计量经济分析方法与建模[m].北京:清华大学出版社,2006.
[3]ruey s tsay.analysis of financial time series[m].潘家柱译. 北京:机械工业出版社,2006.
[4]enders,w. 应用计量经济学:时间序列分析(第2版)[m].杜江,谢志超译.北京:高等教育出版社,2006.
[5]pindyck,r.s. econometric models and economic forecasts(第4版) [m].钱小军译.北京:机械工业出版社,1999.
[6]mills,t.c. the econometric modelling of financial time series(第2版) [m].俞卓菁译.北京:经济科学出版社,2002.
[7]赵进文,王倩.上证180指数的garch族模型仿真研究[j].经济问题研究,2008,(3).

