摘 要:实物期权模型作为创业投资项目价值评估的工具越来越多的得到风险投资机构的认可,如何准确的确定风险水平,成为非常重要的问题。根据各种风险因素影响的现金流的波动来估算项目的波动率,通过分析影响项目现金流的因素,确定现金流的分布,通过蒙特卡洛模拟项目的收益现值和标准差,根据统计原理建立波动率计算模型。关键词:风险水平;波动率;蒙特卡罗
1 常见的波动率确定方法
常见的波动率的确定方法主要有以下几种:
-1.1 现金流对数收益法
现金流对数收益法是根据对未来现金流的估计及相应的对数收益来计算波动率的。首先是对未来现金流的一系列预测,将它们转化为相对收益率,然后再取这些相对收益率的自然对数。这些自然对数收益率的标准差即为即为波动率。即:
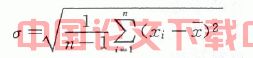
其中xi为某个时段的收益率的自然对数;为所有时段收益率自然对数的期望。
1.2 对数现值法
对数现值法是将未来现金流的估计分为两类,一类是第一个时间段的现值,另一类是当前时间段的现值。假设贴现率是常数10%,所有现金流先是都贴现到时段0,再贴现到时段1,然后分别将这些值加起来,其计算公式为:
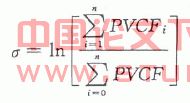
1.3 市场代言人法
该方法利用市场上的公开数据。对于要考查的项目而言,应用市场上的有可比性的公司的公开股票交易价格,这些公司的功能、市场及其风险必须类似于所考查的项目。于是根据股票的执行价格就可以计算出自然对数相对收益的标准差,这种方法与前面提到的未来现金流的对数收益法是一致的。
1.4 广义自回归条件异方差(garch)方法
garch模型主要用来分析股票价格按照时间序列分布的数据,以确定其变化和波动率。garch模型方法计算简便,但是存在缺点:公司的股票价格受到股市上大盘走势、投资者的心理因素以及其他许多与项目本身无关的因素的影响,而且,一家大公司的市场价值是许多相互作用的不同项目组成的,不只跟某一个项目相关。
以上几种方法都存在较大的缺陷。现金流对数收益率法的主要问题是某一时段的现金流有可能出现负值,而负价值的对数是不存在,这种方法在计算金融期权的波动率时较为有效,计算实物期权的波动率存在较大的缺陷;对数现值法的主要缺陷是假定了一个确定的折现率,而这与实际是不相符的;市场代言人法的主要缺陷是市场上很难找到一个项目与所考查的项目的风险水平等因素相似或者相近的项目,尤其创业投资项目大多是高科技项目。
由于上述波动率估算方法的局限性,在利用实物期权方法进行价值评估时,多采用的是经验数据。dixit和pindyck推荐在实物期权中采用每年15%~25%的波动率进行计算,也有学者采用年波动率高于30%的数据进行计算。专家估计法存在人为随意取值的可能性。
2 波动率计算
2.1 基本理论
波动率是对资产价值不确定性程度的度量,波动率越大,项目价值的涨跌幅度就越大。从统计的角度看,波动率可以看作是资产价值变动的标准差。对于上市公司,项目价值由股票价格表示,其波动率即为股票价格对数变动的标准差。
对于非上市的投资项目,价值的评价指标有财务内部收益率、财务净现值、投资利润率、收益净现值等,其中收益的现值能够较好的反映项目的整体情况。但是,投资项目期权价值的波动率不能采用股票价格对数标准差的公式计算,这是因为股票价格可以保证为正数,而项目的净现值不能保证恒为正。
2.2 蒙特卡罗方法
蒙特卡洛模拟方法通过随机变量的统计试验、随机模拟来求解变量的近似解。根据现金流的概率分布和随即数计算抽样值,得到一系列的现金流,根据净现值公式得到n个净现值。根据大数定理,当模拟次数n充分大时,净现值的算术平均值即为其估计值。
本文建议采用管理层假设法解决这一问题。具体做法是:首先通过决策者或专家的经验估计,对影响项目价值的有关变量,如销售收入、投资、经营成本、项目寿命期、折现率等参数用三点估计法或专家的意见的统计结果,给出上述参数的变化区间和概率分布(如正态分布、均匀分布等),利用随机抽样和计算机上千次以上的蒙特卡罗模拟计算,便可计算得出项目收益现值和波动率。此时,项目收益现值v和波动率是同时得出的。
(1)具体的计算过程如下:
①确定现金流的影响因素及其概率分布。②根据概率分布进行随机抽样,模拟各年现金流。③根据模拟的现金流计算若干净现值。④计算平均净现值npv及标准差s。⑤计算波动率σ=s/npv。
(2)举例如下:某企业为开发一种新产品进行一项r&d投资项目,计划在研发阶段初始投入450万元,两年后进行中试再投入1000万元,第四年末再投资2000万元进行市场化开发,将于第五年产品上市并开始取得收益。
根据预测和专家判断,该项目的相关财务参数和收益估计如下:预期该项目产品的寿命为区间数[7,10]年,假定服从均匀分布;项目年销售收入的期望值为3000万元,标准差为600万元,假定服从正态分布,s = n(3000,600)万元;项目年经营成本的估计期望值为500万元,标准差为50万元,假定服从正态分布,co = n(500,50)万元;项目基准折现率取均值为25%,标准差为5%的的正态分布,i = n(25%,5%),无风险利率取一年期的银行贷款利率 r = 7%,全部r&d和市场化开发投资按照直线折旧法在项目寿命期内折旧或均匀摊销,期末残值为零。
以上案例中,利用excel软件和已知数据,进行一次模拟运算过程如下:取产品寿命的随机数,假定是8.04年,取收入、成本、折现率的正态分布随机数,如表1:
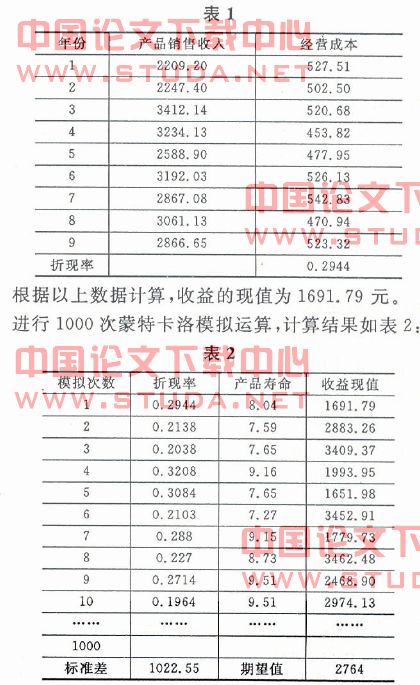
得到折现到该项目期初时的期望收益现值为 v = 2764万元,
波动率σ=标准差/期望值=1022.55/2764 = 37%
3 结束语
相对于金融期权而言,实物期权的计算更加困难。波动率作为实物期权模型里极为重要的变量,在单因素和多因素敏感性分析中,显示该变量具有很强的敏感性,如何有效的确定波动率水平,对实物期权价值的确定有着决定性作用。目前常用的模仿金融期权波动率估算方法在实物期权的应用中存在着局限性。对此,本文通过对影响项目收益的因素进行随机抽样,确定项目的现金流,模拟项目的净现值和标准差,根据统计原理建立波动率计算模型,解决了实物期权评价中波动率估算的难题。
参考文献
[1]graham a. davis, estimating volatility and dividend yield when valuing real options to investor abandon[j]. the quarterly review of economics and finance,1998,38(special issue):725-754.
[2]dixit a k,pindyck r s. investment under uncertainty[m].princeton:princeton university press,1994.

