摘要： 随着人民生活水平的提高，建筑给排水工程设计中的直饮水系统也越来越多，工程设计中直饮水管道的秒流量 计算 也就显得比较重要了。

关键词： 直饮水 概率 使用概率 设计秒流量 函数 类 循环体

随着人民生活水平的提高，建筑给排水工程设计中的 直饮水 系统也越来越多，工程设计中 直饮水 管道的秒流量计算也就显得比较重要了。

《2003全国民用建筑工程设计技术措施给水排水》中第3章第62页对 直饮水 管道的设计秒流量计算采用的是概率法进行计算。其计算步骤如下：

1.先计算出系统的最高日用水量q_d：q_d=n×q_d

式中：n—系统服务的人数 q_d—用水定额（l/d.人）

2.再计算出系统最大时用水量q_h：q_h=k_h×q_d÷t

式中：k_h—时变化系数 t—系统中 直饮水 使用时间（h）

3.然后计算出饮用水龙头的使用概率p：p=α×q_h÷(1800×n×q₀)

式中：α—经验系数，取0.6~0.9（一般取0.8） n—龙头数量

q₀—龙头额定流量（l/s）

4.根据使用概率p，求出瞬时高峰用水量龙头使用数量m：

5.求出瞬时高峰用水量q_s：q_s=q₀×m

在上述5个计算步骤中，第4步的计算在饮用水龙头数量少 时尚 可手算。如果龙头数量≥12个时，手算就很麻烦了。为此，书中特意列出了表3.1.9-3 《龙头设置数量达12个以上时的使用数量》。表中对于使用概率为0.005的整数倍进行详细列表，并且表中的数量仅局限于1500个龙头。在实际工程计算中，计算出的使用概率是0.005的整数倍的可能性是很小的，对于小数量的龙头，采用内插法求解时其误差可以忽略不计；但是数量大时，其误差 影响 就比较大。为此，我在利用程序求解方面作了一些尝试。

在上述5个计算步骤中，第4步是整个计算过程中最难求解的一步。瞬时高峰用水量龙头使用数量m是在n个龙头中，若0~m个龙头使用概率的总和不小于0.99，则m为设计秒流量发生时的同时使用龙头个数。

在n个龙头中，任意r个同时使用的概率为p_n^r：

p_n^r=c_n^r×(1-p)^n-r×p^r

式中：c_n^r为从n个不同元素中，每次取出r个不同的元素，不管其顺序组合成的组合数量：

c_n^r=n！÷ (r！× (n-r)！)

在n个龙头中，任意0~m个水龙头使用的概率总和不小于0.99，其表达式为

p_n=∑_r=0^mc_n^r×(1-p)^n-r×p^r

因此，我们只要按r从0到m依次求出p_n^r以及p_n，并判断p_n是否满足≥0.99；如果是，则m的值就是我们所求的解。具体编程流程如下：

在上述编程流程中使用了一个do while循环，并加了个计数器。这样，在满足条件跳出循环的时候，就可以得到m的值。

但是在计算程序执行过程中，由于vb编程 软件 自身对于计算结果的限制，对于c_n^r=n！÷ (r！× (n-r)！)中的组合数，如果采用integer变量，很容易就超出可计算的范围；如果采用long变量或double变量，则占用内存较多，且计算范围并未扩大很多。鉴于以上情况及所计算的概率值≤1，我考虑利用vb6提供的log函数(即数学函数中的ln)，对上述公式进行了转换：

㏒(c_n^r)=㏒(n！)- (㏒ (r！)+ ㏒ (n-r)！)

㏒(p_n^r)= ㏒( c_n^r)+ (n-r)㏒(1-p)+r㏒(p)

因此在程序中，需要专门设计两个新的类：第一个类，用来处理㏒(p_n^r)，其源程序如下：

function lnjc(n as integer) as double

dim tempjc as double

tempjc = 0

do while n >= 1

tempjc = tempjc + log(n)

n = n - 1

loop

lnjc = tempjc

end function

第二个类，用来处理㏒(c_n^r)，其源程序如下：

function lncjc(n as integer, r as integer, p as double) as double

dim tempcjc, temp0, temp1, temp2 as double

dim n1 as integer

dim nn, rr as integer

dim temp as new lnjc

tempcjc = 0: nn = n - r: n1 = nn: rr = r

if r <= 0 the n r = 1

temp0 = temp.lnjc(n)

temp1 = temp.lnjc(r)

temp2 = temp.lnjc(n1)

tempcjc = temp0 - temp1 - temp2

temp1 = rr * log(p)

temp2 = nn * log(1 - p)

temp0 = tempcjc + temp1 + temp2

lncjc = temp0

end function

然后再用vb6中提供的另一个函数exp进行反向求解，既可以得到p_n^r。上述两个类在do while循环体内，然后再计算p_n=∑_r=0^mp_n^r，退出循环体的条件是：

p_n是否满足≥0.99

其循环体的求解源程序如下：

private sub command3_click()

dim n as integer

dim r as integer

dim m as integer

dim nn, mm as integer

dim p as double

dim p0 as double

dim temp as new lncjc

if text2.text <> "" then fwrs = cdbl(text2.text)

if text4.text <> "" then ysde = cdbl(text4.text)

if text5.text <> "" then n = cint(text5.text)

if text7.text <> "" then jyxs = cdbl(text7.text)

if text9.text <> "" then edll = cdbl(text9.text)

if text3.text <> "" then

bhxs = cdbl(text3.text)

yssj = cint(yssjt.text)

p = log(jyxs * (bhxs * fwrs * ysde / yssj)) - (log(1800 * edll) + log(n))

p = exp(p)

text1.text = format(p, "0.###0")

else

p = cdbl(text1.text)

end if

if n <= 32000 then

p0 = 0: mm = 0: nn = n

do while p0 < 0.99

m = mm: n = nn

p0 = p0 + exp(temp.lncjc(n, m, p))

mm = mm + 1

loop

text6.text = mm - 1

text8.text = format(((mm - 1) * edll), "0.##0")

else

msgbox ("龙头总数量不能超过32000个！")

end if

end sub

这样，计算的龙头数量可以多达32000个龙头。对于较大的住宅小区，已经是足够用了。程序运行时的界面如下：

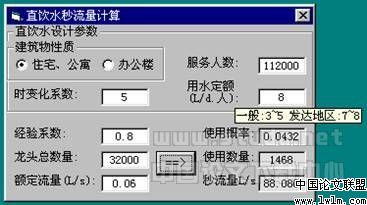
其窗体调用时的源程序如下：

private sub form_load()

command3.enabled = false

end sub

对于建筑物性质，其参数控制的源程序如下：

private sub option1_click(index as integer)

select case index

case 0

yssjt.text = 24: text3.tooltiptext = "4~6": text4.tooltiptext = "一般:3~5 发达地区:7~8"

case 1

yssjt.text = 10: text3.tooltiptext = "2.5~4.0": text4.tooltiptext = "2~3"

end select

end sub

在上述的程序中，在可选参数设置了提示(如上图)，使用户界面更具人性化；类function lncjc(n as integer, r as integer, p as double) as double中调用类function lnjc(n as integer) as double，对 计算 程序进行了压缩；计算32000个龙头的过程在pii 466mhz的机器上约需运行一分钟，即可以得出计算结果。

下面，我们们验证一下计算结果：

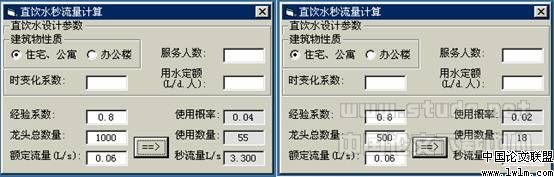
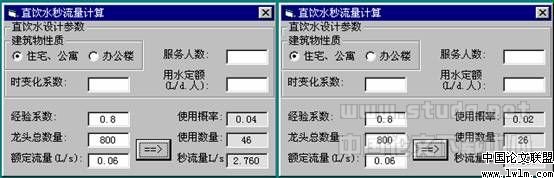
上述计算结果如下表：

龙头数量 使用概率 使用数量 龙头数量 使用概率 使用数量 龙头数量 使用概率 使用数量 龙头数量 使用概率 使用数量 500 0.02 18 800 0.02 26 800 0.04 46 1000 0.04 55

上表中的计算结果与表3.1.9-3中的结果吻合得很好。

因此， 应用 计算机编程技术可以大大减少人工计算量并提高计算的准确性和计算速度，从而能为设计提供一个强有力的辅助工具。

引用资料：isbn7-80177-168-0/tu.085《2003全国民用建筑工程设计技术措施给水排水》建设部工程质量安全监督与行业 发展 司