摘  要  访问控制是一种很流行的信息保护机制，被广泛应用在信息系统中。十多年来，在这个领域已取得了很多成就。传统的访问控制已经被更加灵活强大的系统代替了，如基于角色的访问控制(rbac)和灵活授权框架(faf)。但是，在访问控制系统中，对系统管理员的绝对信赖一直是对信息安全的潜在威胁。为了克服这个威胁，分等级的加密被发展作为访问控制的替补方法。通过使用分等级的加密，信息系统中的所有信息被加密：由低层安全类加密的数据可以被高层的安全类解密。文章描述了基于数据和基于密钥的两种加密方法实现加密的访问控制。      关键词  加密；解密；访问控制；等级  

1  引言

     分等级进行加密的想法最早是由akl和taylor提出的^[1]，多级系统中的主体(用户)和客体(数据)有各自的安全级，用户对数据的访问必须满足一定的安全性要求。安全级是一个二元组<密级，分类集合>。用户间的安全级的比较是按偏序进行的。如果安全级u₁=密级l₁分类集合s₁，u₂=密级l₂分类集合s₂。称u₁<=u₂当且仅当l₁<l₂且s₁⊆s₂。      假设有主体s，客体o₁、o₂和o₃，如果安全级uo₁<=u_s，u_s= uo₂，u_s<=u_o3，则s对o₁只能读，对o₃只能写，对同安全级别的客体o₂可以进行读写两种操作。在这种多级安全模型中，一个主体(用户)访问其它主体的数据时，只需要与被访问主体的安全级进行比较，如果访问主体的安全级比被访问主体的安全级高，则允许访问，否则，访问被禁止。从中可以看到，如果非法用户篡改安全级，则很容易实现对其它(高安全级)用户数据的非法访问。可见这种比较安全级的访问控制方法具有潜在的不安全性。通过加密方法可以有效消除这种不安全性。首先，在对用户身份鉴别时，不仅生成用户密码，同时还为用户生成一个公钥、私钥对，利用密钥对来加强对用户身份鉴别，再利用用户的私钥为用户生成一个访问密钥，由此来实现访问控制。

2  基于数据的解决方法

     找到足够安全的保护数据的方法或者安全的产生访问密钥的方法，就可以解决访问控制的问题，这是实现加密访问控制时的重点。      非常流行的加强访问控制的方法是通过访问控制列表。每个数据都与一个acl表相关，表中列举出授权的用户组和相对应的访问模式。通过查看acl，很容易决定允许谁对相关数据进行对应操作。acl包含通常情况下的所有访问控制。例如，它支持等级访问控制。如果我们根据等级结构或者组织产生acl。那么等级访问控制就能够被加强。也就是说，一个数据拥有这和它所有的祖先都被在它的数据acl中列举出来。

图1  访问控制列表(acl)

        从加密的角度来讲，为了加强通用的访问控制，每个数据必须被加密，这样只有acl中的主体有能力解密数据。假设每个主体被分配一对密钥：公钥和私钥。k个主体共享消息m：s₁，s₂，…s_k，对于每个主体s_i∈{ s₁，s₂，…s_k }，m被si的公钥加密。加之它所有者的密文，m被加密（k+1）次。为了共享一个单一的信息m系统保存（k+1）个密文。这种方法的消极面出现确定了，也就是存 储加密数据的多个副本可能会产生矛盾(不一致性)。

2.1  系统元素

     我们的基于数据的解决方法包括以下元素：      主体s={s₁，s₂，…s_l}，主体既可以是用户也可以是组。      公钥密码系统包括三个功能函数：      （1）密钥生成函数kg：∀s_i∈s，kg生成一对密钥：公开密钥ksi和它的对应的私有密钥ks_i^-1。      （2）加密函数e：c=e_k(m)，其中c是密文，m代表信息，k表示公开密钥(加密密钥)。      （3）解密函数d：c=d_k^-1(c)，k^-1表示私有密钥(解密密钥)。

2.2  加密的访问控制

     假设主体s_i想与k个用户s_i1，s_i2，…，s_ik∈s共享信息m，s_i执行下面的操作(为简单起见，我们假设m<n_s1，n_s2，…n_sl)。如果是长信息，可以一块一块的进行加密。      （1）首先，s_i计算k个单一的密文，也就是说，对于∀s_j∈{s_i1，s_i2，…，s_ik}，计算e_{k sj} (m)。      （2）然后，s_i用加纳法则计算出crt的解x，0≤x ≤ns_i1，ns_i2，…，ns_ik，x同时满足以下k个式子：                            (1) x ≡e_{k s1}(m)mod ns_i1.                            (2) x ≡e_{k s2}(m)mod ns_i2.                                    …                            (k) x ≡e_{k sk} (m)mod ns_ik。                            (3) 把s_i保存在sdb里。对每个访问m的主体s_j，s_j∈{s_i1，s_i2，…，s_ik}，s_j需要计算e_{k s j}(m)＝x mod ns_j。然后s_j使用私钥e_{k sj}^-1恢复m。

2.3  授权变更

     数据项授权的变更，如一个主体被授权/撤消对数据项的访问，在信息系统中是很常见的事情。我们的基于数据的解法根据受到影响的数据状态来控制授权变更。如果数据项是动态的(也就是说数据在授权变更时有变化)，a1到a3的所有操作基于授权主体新的组再执行一次。如果数据是静态的(也就是说授权更改时数据项不发生改变)。

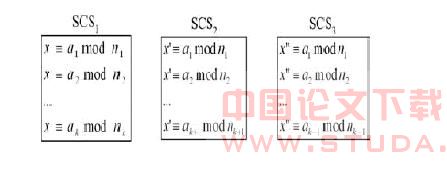
图2  scs

 

     图2中scs₁包括k个同时满足的等式，它的crt解是x；给scs₁增加一个条件等式得到scs₂，它的crt解是x′；从scs₁去除一个条件等式得到scs₃，它的crt解是x″。假设x的值已经算出来了，为得到x′的值，我们只需要找到x′≡x mod n₁n₂和x′≡a_k+1 mod n_k+1两个等式的crt解。为得到x″的值，我们只需要一个模运算：x″= x mod n₁n₂…n_{k +1}。总之，x′和x″的值可以很容易得从x得出^[2]。      在我们的基于数据的解法中，准予一个主体对一个静态数据项进行访问与从scs₁到scs₂的转换是等价的。新的共享密文x′可以从旧的共享密文x有效得到。撤消一个主体对一个静态数据的访问与从scs₁到scs₃的转换是等价的。通过一个模运算可以简单的从旧的密文x得到新的密文x″。

3  基于密钥的解法

3.1  实现      在基于数据的解法中，k个共享者共同分享信息m，共享密文的大小是原始信息m大小的k倍。因此基于数据的解法在m或者k很大的情况下是不可取的。而且，基于数据的解法是基于公开密码系统的。这样的话，共享一个数据项，数据项的所有者必须知道所有分享者的加密密钥。为保护解密密钥的机密性，我们只能使用公开密钥加密系统。公开密钥加密系统比对称加密体制慢。      我们的基于密钥的解法的主要思想是：不是分享信息，而是分享加密密钥^[3]。除了在基于数据的解法中列举的元素外，基于密钥的解法还需要一个对称密钥加密系统。这里，我们用se表示加密函数，sd表示解密函数。      如果一个主体s_i 想与主体s_i1，s_i2，…，s_ik∈s分享信息m，执行如下操作：      （1）随机选择一个对称密钥k_r。      （2）使用k_r 加密m：c=se_kr(m)。      （3）∀s∈{s_i1，s_i2，…，s_ik}，计算e_ksj(k_r)。      （4）找到同时满足下面等式的crt解：                      (1) x ≡e_{k si1}(k_r)mod ns_i1.                      (2) x ≡e_{k si2}(k_r)mod ns_i2.                              …                      (k) x ≡e_{k sik} (k_r)mod ns_i 。                      (5) 把x||c保存到sdb中，其中符号“||”的意思是“串联”。 主体s_j∈{s_i1，s_i2，…，s_{i k}}访问m，sj需要计算e_{k sij}(kr) = x mod n_{s j}；然后用私钥ksj^-1取回对称密钥kr，也就是kr=d ksj^-1(e_{k sij}(kr))；最后，使用kr恢复明文m，m=sd _kr(c)。

3.2  授权变更

     对于动态数据，任何时候只要授权发生更改，从(1)到(5)的步骤都要被基于新的主体组重新执行一次。对于静态数据，如果主体被撤消了对数据的访问，为组织主体使用旧的对称密钥获取数据，从(1)到(5)的步骤都要被基于新的主体组重新做一遍。如果一个主体被准予对数据的访问，不需要对数据重新进行加密，因为旧的对称密钥仍然可以使用。因此从scs₁到scs₂的转换可以被使用来从旧的对称密钥产生新的共享密文。新的授权主体可以获取旧的对称密钥来截密数据^[4]。      因为对称密钥的大小通常比数据项小得多，公开密钥加密比基于数据的解法更加有效。由于同样的原因，共享密文的大小比基于数据的方法小很多。总之，当数据或者分享者数目较大时基于密钥的解法更可取。

3.3  siff函数实现

     如果能找到足够安全的产生访问密钥的方法，则可以容易解决访问控制的问题，可以利用siff函数实现^[5]。 先作如下假设：      (1) 用idi表示节点ni的标识，设idi能用 l(n)位长的串描述，l是多项式。     (2) f={fn|n∈n}是伪随机函数族，其中fn={fk| fk：∑^l(n) →∑ⁿ，k∈∑ⁿ }，用n位的串k来标识f_k。      (3)h={ hn|n∈n }是k-siff，将n位的输入映射为n位的输出。设k足够大，足以表示一个节点拥有的父节点数。      下面给出一个生成访问密钥的算法：      算法：访问密钥生成算法      输入：用户节点集{n1，…ni，…np(n)}   输出：各用户对应的访问密钥{k₁，…ki，…kp(n)}      (1)如果节点n₀是最大节点，k₀=fpk₀(id0)；其中pk₀是节点n₀对应的用户的私钥。否则转(2)。      (2)如果节点nj只有一个父节点ni，ni已经有了访问密钥ki，则nj的访问密钥kj(n位长)：kj=f_ki(idi) 。      (3)如果节点nj有多个(如：p个)父节点：ni1，ni2，…，nip，对应有各自的访问密钥k_i1，k_i2，…k_ip，则k_j为从随机选取的n位串：k_j∈_r∑ⁿ，再从hn中随机的选取一个哈希函数hi，使得将f_kj1(idj)，f_kj2(idj)…，f_kjk(id_j)都映射到k_j。即： hi((f_kj1(idj))= hi((f_kj2(idj))=…= hi((f_kjp(idj))=kj。然后公开哈希函数hi，使之对n_j 所有的祖先节点都可用。      (4)如果节点集中的节点全部访问完毕则输出访问密钥，算法结束；否则转(1)。 由算法可知，如果ni≥nj，则kj 总可以由ki得到。当ni是nj的的单一父节点时，k_j=f_ki(id_i)；当ni不是nj的父节点时，通过从上往下的一条路径ni最终也能得到kj。

4  结论

     文章综述了用加密来解决访问控制的方法，描述了基于数据的和基于密钥的解决方法。文中系统的安全性是基于不同的函数：中国余数定理和siff函数实现的。

参考文献

     [1]  王元珍，魏胜杰，朱虹. 安全dbms中访问控制的一种加密解决方法. 计算机工程与应用. 2003(16)，pp：195-197      [2]  yibing kong，jennifer seberry. a cryptographic solution for general access control. janusz r. getta，springer-verlag berlin heidelberg 2005. pp：461-473      [3]  ray，i.，ray，i.，narasimhamurthi，n.. a cryptographic solution to implement access control in a hierarchy and more. proceedings of the seventh acm symposium on access control models and technologies. acm press (2002)，pp：65-73      [4]  jajodia，s.，samarati，p.，sapino，m. l.，subrahmanian，v. s.：flexible support for multiple access control policies. acm transactions on database systems，vol. 26，no. 2. acm press (2001)，pp：214-260      [5]  akl，s. g.，taylor，p. d.：cryptographic solution to a multilevel security problem. advances in cryptology：proceedings of crypto ’82. plenum press (1982)，pp：237-249