摘 要 本文针对软件项目中的风险问题,根据信息熵给出项目各风险因素的重要性评价并且利用支持向量机评估软件项目的风险类别,此方法完全依赖数据进行客观分析,排除了人为的主观因素,因此其结果优于利用模糊综合评判方法得出的结果。
关键词 软件项目;风险;信息熵;支持向量机;
1 引言
软件风险是指软件开发过程中及软件产品本身可能造成的伤害损失,由于软件项目开发和管理中存在着诸如技术、内部管理及外部环境等种种不确定因素, 使软件行业成为高风险的产业,如果风险变成了现实,就会产生恶性后果或损失,因此应对软件项目风险进行评价以便于更好地进行软件项目地开发及管理。目前的风险评价及分析方法主要有调查和专家打分法、模糊数学法[1]、层次分析法[2],定性方法、基于树的方法;专家打分法、模糊数学法、层次分析法人为因素多而且手工计算繁琐。定性方法用于辨识系统中的潜在危险和失效是有效的,但缺乏考察事件之间依赖性的能力。基于树的方法弥补了这一缺陷,考虑了事件之间的依赖关系,但基于树的方法主要用于找出导致不期望事件的截集,然而这种方法只能用于事故场景的静态、逻辑的建模,并且影响人类行为的因素不能被明确地建模,这就影响了事件之间独立性的评估。本文提出的信息熵的方法用来对软件各个风险因素重要性进行计算,它具有运算量小,结果直观易解释以及易评估的性质,排除了人为的主观因素。
本文利用支持向量机(support vector machine简称svm)方法来预测软件风险,它是建立在统计学习理论的vc维理论和结构风险最小原理(srm)基础上[3]。兼顾训练误差和泛化能力,根据有限的样本信息在模型的复杂性和学习能力之间寻求最佳折衷。在解决小样本、非线性、高维数、局部极小值等模式识别问题中表现出许多特有的优势。因而在许多领域得到了成功的应用。同时,为了评估各个风险因素的重要程度,本文采取了信息熵的方法,这种方法具有计算量小和易解释性,弥补了专家打分法中因人为因素造成的主观性。
本文其它内容如下。第二部分介绍软件项目风险评价指标体系的建立,进而从各个侧面较完整地反映出软件项目的风险。第三部分和第四部分分别描述了基于信息熵的软件项目各风险因素的重要性评判以及基于支持向量机的软件项目风险类别的评估。第五部分是根据建立的模型利用数据进行实例研究。第六部分对本文进行了总结。
2 软件项目风险评价指标体系的建立
软件项目的风险评估指标应能从各个侧面较完整地反映软件项目的风险,同时需要按照一定的标准将风险分类。在软件项目开发过程中,一般有以下六个风险因素会直接影响软件的风险,分别如下:
1)软件产品规模(f
1)
根据以往开发项目的经验所知项目的风险是直接与产品的规模成正比的。软件产品规模有以下几个因素决定:产品规模估算的信任度、软件产品的用户数、复用的软件数、产品规模与以前产品规模平均值的偏差。
2)业主需求(f
2 )
每位业主都有自己不同的需求,开发商为了满足不同业主的不同需求。决定业主需求的因素有:业主供应条目或信息、内部或外部转包商的关系、交互成员或交互团体依赖性、经验丰富人员的可得性。
3)软件项目需求分析(f
3 )
软件项目需求分析就是分析人员在用户和软件设计人员的配合下对自己生成的需求规格说明和初步的用户手册进行复核,以确保软件需求的全面性、精确性和一致性,若此工作进行不好,就会对项目的成功造成很大的阻碍。主要包含以下几个方面的风险因素:产品需求的认知程度、需求分析中客户的参与程度、需求变化的分析程度、安全性及可靠性需求的分析程度。
4)技术(f
4 )
技术对于一个软件项目的顺利完成是至关重要的,所以说如果技术出现问题那么就会引发一系列的风险问题。主要有下面这些风险因素:对方法、工具的使用状况、应用领域的经验状况、系统的稳定性状况。
5)开发方式与开发环境(f
5 )
开发方式和开发环境风险是由于软件项目所处的环境与自身的开发方式状况而导致实现软件项目预期目标中所带来的不确定性。主要风险因素有:软件项目团队的稳定性、项目过程的控制程度、项目资金的稳定程度。
6)人力资源管理( f
6)
人力资源管理风险是由于在软件项目开发过程中由于对开发人员及相关人员管理不当及管理混乱从而对软件项目开发造成的风险。其主要的风险因素包括:人员职能设置之间的协调性、项目所有者与决策者的关系。
总体项目的风险等级分为3个类别,分别为风险较小(y=1 )、风险一般( y=2)、风险较大(y=3)三类。在所建立模型中,总体项目的风险等级对应于y的取值,而六个风险因素——软件产品规模、业主需求、软件项目需求分析、技术、开发方式与开发环境、人力资源管理所属的风险类别对应于六维向量x的取值。
3 基于信息熵的软件项目各风险因素的重要性评判
设已知有n个软件项目,矩阵
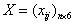
的列向量x
j表示各项目的风险因素f
j(j=1.2...6),行向量x
i表示每个软件项目(i=1.2,...n),要衡量每个风险因素f
j(j=1.2...6)的重要性,本文利用信息论中信息熵的方法来评判。列向量
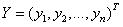
中的分量
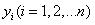
分别表示第i个项目的风险等级:y
i=1表示第i个项目的风险等级较小, y
i=2表示第i个项目的风险等级一般, y
i=3表示第i个项目的风险等级较大。则
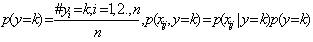
对于项目的风险等级 f
j,它的熵为
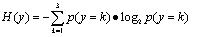
;
对于项目各风险因素 f
j,它的熵为

;(
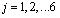
)
对于项目各风险因素 f
j中在各个风险等级的风险为:
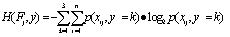
;(
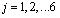
)
则各风险因素 f
j的重要性评分为:
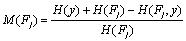
;(
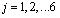
)
越高表示该因素重要性越高。
4 基于支持向量机的软件项目风险类别的评估
支持向量机是一种分类方法,假定软件项目风险评估问题
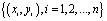
,其中x
i(i=1.2,...n)代表第 i 个项目的六个风险因素,为六维向量,
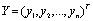
代表每个项目的风险类别,最简单的线性分类器是希望找到一条直线,
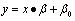
其中β
n为一个数量β为一个六维向量,这样对一个新样本 x' 的分类可以用
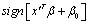
来表示。为此还需要解决如下问题:
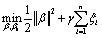
使得
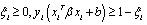
支持向量机很容易就可以用来解决多点分类问题,实际运用中支持向量机可能不是线性的,它通过核函数将原来的样本映射到另外一个核空间中,这里我们对核函数不做深入讨论,我们选择了线性核函数在本文的研究中,先从已有的软件项目数据作为训练样本来训练支持向量机,然后用训练好的支持向量机来预测新的软件项目样本,从而进行准确性验证。
5 案例研究
为了验证本文提出的算法的有效性,我们用matlab生成了模拟数据。假设每个项目可以用一个六维向量表示:
对于风险小的类别,即 y=1时,软件的六个风险因素符合期望分别为
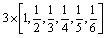
,每个分量的方差分别为1的正态分布。
对于风险一般的类别,即 y=2时,软件的六个风险因素符合期望分别为
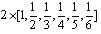
,每个分量的方差分别为1的正态分布。
对于风险很大的类别,即 y=3时,软件的六个风险因素符合期望分别为
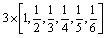
,每个分量的方差分别为1的正态分布。
本文对每个风险等级类别随机生成了100个样本,这样总共有300个样本。比如对于风险因素f
1软件产品规模,假设软件产品规模是一个随机变量,在风险较小的情况下软件产品规模也比较小,所以按照以上假设,它符合一个n(1,1) 的正态分布;在风险一般的情况下,软件产品规模适中,按照以上假设它符合一个 n(2,1) 的正态分布,同理在风险较大的情况下软件产品规模也非常大,用n(3,1) 的正态分布表示。均值的大小体现了在不同风险等级下软件的平均规模。对于其他因素的均值也可以类似理解。则显然可以推出风险因素的重要性排序应该是:
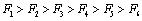
应用文章中信息熵的方法计算出每个风险因素的分值。为了计算每个风险因素f
j的重要性评分,我们取出x
j的最大值max和最小值min ,然后将值区间分为10等分,得出风险因素 落入每个值区间的概率,这样就把一个连续的随机变量转化为一个离散的随机变量来计算,从而得出信息熵。表1显示其运行结果。
表1 各项目风险因素的重要性

每个风险因素的评分给出了该风险因素的一个重要性评估,此方法成功的给出了一个正确的评估。根据这个结果可以说明:软件产品规模( f
1)在软件项目的重要性评分为0.088706,业主需求(f
2)在软件项目中的重要性评分为:0.029911,软件项目需求分析(f
3)在软件项目中的重要性评分为:0.021996,技术(f
14)在软件项目中的重要性评分为:0.020708,开发方式与开发环境( f
5)在软件项目中的重要性评分为:0.015648,人力资源管理(f
6 )在软件项目中的重要性评分为:0.012043,从而可以认为在软件项目管理中对软件产品规模的控制的重要性比对人力资源管理的重要性大得多,那么在进行软件项目开发时可以通过加强对软件产品规模此风险因素的管理来更好地控制软件项目开发的风险。由于该模拟数据不适合做svm分析,因此本文不对模拟数据进行svm分类.
第二部分:下面利用其他项目的数据[3]来进行分析,在这个数据集中,每个风险因素对应5个等级,分别对应0.1,0.3,0.5, 0.7,1,每个值都有专家评分取得。该数据集中有14个数据,利用其中的10个作为训练数据,4个作为测试数据。数据如表2所示。
表2 样本项目的各个指标及项目风险水平值
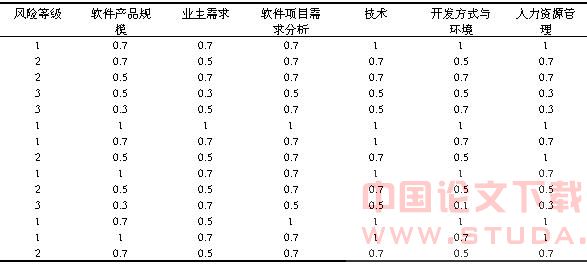
为了评估svm的有效性,随机地从14个数据中取出10个作为训练数据,剩下的4个作为测试数据,总共进行了12次这样的随机选取,发现在10个训练数据上的训练正确率均为100%,而平均测试正确率为97.92%,效果非常好,显示出此方法可以非常可靠地对软件项目风险进行评估,同时用这14个数据得出了每个项目风险因素的重要性对比,如表3所示。
表3 各项目风险因素的重要性

由上面结果可以发现,技术因素的值为1,这表明技术可以完全决定软件项目风险等级,说明了技术在软件项目开发中的重要性,同样,人力资源管理在软件项目风险管理中的作用也不可忽视。
6 结论
本文不仅利用了svm来预测软件项目风险,而且给出了各个风险因素的评估。虽然在对软件项目风险因素重要性进行分析的方法中,本文只是采取了简单的方法对连续变量进行了离散化,这个过程中可能会有一些信息丢失,但根据实验结果说明本文的方法在此数据集上具有效率高、预测准确和可靠性高的特点,因此在今后的学习中会提出更好的算法以得到更好的离散化变量。同时为了进一步完善风险预测的支持向量机方法,今后将会利用更多的数据集测试算法并对支持向量机作交叉验证,找出该方法的优缺点,以求能有进一步地提高。
参考文献
[1]冷晓彦.企业信息化项目风险的模糊综合评价[j].情报科学,2005,23(7):977-981.
[2]张丰,李红梅.层次分析法在风险投资项目评估中的应用[j].商业研究,2005,24(332):12.
[3]张丽霞,施国庆.基于支持向量机的工程项目风险预测研究[j].计算机工程与应用,2005,21:224-226.
[4]jacek biesiada, w_odzis_aw duch, adam kachel, krystian m¸aczka, sebastian pa_ucha, feature ranking methods based on information entropy with parzen windows [c], katowice,poland, international conference on research in electrotechnology and applied informatics, august 31, september 3, 2005:2.

