摘  要  介绍了应用最小二乘法对t-s结论参数进行粗略辨识，确定参数的大致范围，再应用遗传算法对前提参数和结论参数同时优化的参数辨识方法。对非线性函数进行逼近实验，给出了用matlab编程进行仿真的具体实现方法，结果证明该方法的可行性和有效性。     关键词  最小二乘法；参数辨识；遗传算法  

0  引言

    对t-s模糊系统参数辨识的过程大致分为结构辨识和参数辨识，而参数辨识则是整个系统辨识的关键所在。遗传算法以其在解空间内进行高效启发式搜索，寻优速度快，不易陷入局部最优解等优点成为近来应用较多的优化方法。将遗传算法用于解决t-s模糊模型的参数辨识问题，在应用最小二乘法进行粗略辨识的前提下，用遗传算法对结论参数进行寻优，用matlab进行仿真，取得了较好的效果。

1  用最小二乘法对t-s模糊模型参数的初步辨识

    t-s模糊模型辨识的过程一般分为以下几个阶段：前提结构辨识；前提参数辨识；结论结构辨识；结论参数辨识，直到模型满足要求为止。结构辨识的方法，在此不再详细说明，只对结论参数辨识问题展开讨论。     在确定了前提结构和结论结构之后，对模糊模型的结论参数进行粗略的辨识，以确定遗传算法寻优的范围。在众多的参数辨识方法中，最小二乘法是最基本的一种，gauss于1795年就用最小二乘法，由观测结果估算了行星的运行轨道。此后，这种方法被广泛应用，并根据实际问题提出了许多改进的最小二乘法，如正交最小二乘法，广义最小二乘法，增广最小二乘法等。这里所用的是线性最小二乘法，将前提结构划分的各个范围中的输入输出数据拟合为一次多项式函数。从而得出粗略的结论参数。以此来大致确定遗传算法要优化的结论参数范围。前提参数的大致范围可根据所选的隶属函数来确定。     为简单起见，考虑一维的单输入非线性系统。对下列函数进行逼近[1]： 设定输入范围为[-1，1]，将它模糊分割为五个区，隶属度函数采用广义的钟形函数，这里只有一个输入变量，输出为y = a x + b的线性方程，待优化的结论参数有2×5 = 10个，用matlab编程来初步得出待优化的结论参数，主要代码如下：     data_n=100;newdata_n=1001;x=linspace(-1，-0.6，data_n);     y=0.7*sin(pi*x)+0.3*sin(3*pi*x)+0.1*sin(5*pi*x);     polyfit(x，y，1)     由上述方法仿真可得出的10个参数，确定参数范围，如表1中所示：
表1 用最小二乘法估计的参数及优化所选的参数范围 参数 a₁ b₁ a₂ b₂ a₃ b₃ a₄ b₄ a₅ b₅ 估计参数 -0.6499 -1.0459 0.9010 0.0518 8.3065 0.0000 0.9010 -0.0518 -0.6499 1.0459 参数范围 [-5，5] [-5，5] [-5，5] [-5，5] [-2，15] [-5.5， 5.5] [-5，5] [-5， 5] [-5.5， 5.5 ] [-1，5 ]

2 用遗传算法来优化t-s模型的结论参数

    由于同时优化的参数的数量较多，故采用实数编码的方式对参数进行编码。编码过程是通过计算机产生所要优化的参数范围内的随机数，对每一个参数进行编码后，连接在一起形成一条染色体，然后就可以对它进行遗传操作。用matlab编程，确定寻优范围的主要代码如下： minx(1)=-5.0*ones(1); maxx(1)=5.0*ones(1); minx(2)=-5.0*ones(1); maxx(2)=5.5*ones(1); ．．．．．． minx(10)=-1*ones(1); maxx(10)=5*ones(1); kpar(：，1)=minx(1)+(maxx(1)-minx(1))*rand(size，1); kpar(：，2)=minx(2)+(maxx(2)-minx(2))*rand(size，1); ．．．．．． kpar(：，9)=minx(9)+(maxx(9)-minx(9))*rand(size，1); kpar(：，10)=minx(10)+(maxx(10)-minx(10))*rand (size，1);     在产生大种群后，对个体进行初步筛选，去掉一些适应度差的个体，剩下的作为初始种群进行遗传操作，这种方法可以使种群在保持多样性的同时，节省计算时间。进化代数的确定，一般是根据问题所要求的精度来确定，精度低，进化的代数就可以少一些，反之则多一些。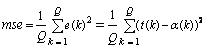     适应度函数是衡量个体优劣的指标，为了达到寻优的目标，适应度函数一般是通过目标函数变换而来的，这里对t-s模型的参数进行辨识，采用的目标函数为均方误差：        （1）     其中：t(k)为由辨识的模糊模型计算出的第k个采样时刻的输出值，α(k)为第k 个采样时刻的实际输出值，q为总的采样次数。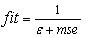     在进行选择操作时，是按照适应度越大，被选择的概率越大，所以，这里选用的适应度函数为：           （2）     其中ε是一个较小的正实数，目的是为了避免除数为零的情况发生^[3]。其主要代码如下： for i=1：1：size  %以下为初始筛选         cansu=kpar(i，：);         code=cansu;         rmse=computeitae(code);%计算均方误差;         bsj=rmse;         bsji(i)=bsj;%将均误差赋给bsji     end         fi=1./bsji;% 求适应度的值     [oderfi，indexfi]=sort(fi)%对适应度值由小到大排列        sortrsa=kpar(indexfi(size)，：);     for s=2：1：selectsize          shuijirsa=kpar(indexfi(size-s+1)，：);         sortrsa=[sortrsa  shuijirsa];          end          sortrsa          kpar=sortrsa          size=selectsize     遗传操作一般包括选择，交叉和变异。选择方法采用蒙特卡罗法，按比例的适应度分配。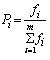若某个个体i ，其适应度为f _i ， 则其被选择的概率表示为：                （3）     由于在进行遗传操作前，已经对个体进行了初步的筛选，所以为了避免对种群中优良个体的破坏，这里采用单点交叉的方法，随机选择交叉点之后，将两个个体的交叉点后面的基因进行交换。变异采用实值变异的方法，随机选择染色体的某个基因，由于用实数编码的方法，每个基因就是一个要辨识的参数值，所以可以用一个函数实现在参数范围内适当改变该参数值的大小，从而达到保持种群多样性的目的。为了使寻优不过早的收敛到次优解，随着进化代数的增加，需要适当增大变异率，其实现方法只需用一个函数来表示变异率： pm=0.1 + [1：1：g]×0.1/g       （4）     式中：pm表示变异率，g代表进化代数。[1：1：g]表示一个数组，变化的范围为[1，g]，步长为1。为了避免破坏优良个体，变异率不宜取的过大。通过实验得知，在第一代时，可取变异率pm=0.1+1×0.1/g，第二代时，变异率pm=0.1+2×0.1/g，以此类推。这样随着进化代数的增加，pm也随着增加。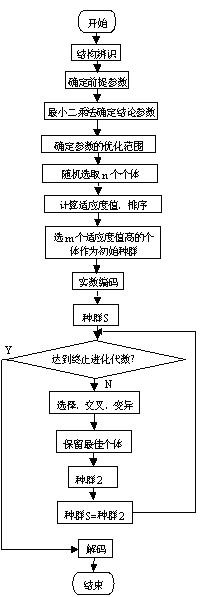     另外，为了防止遗传操作对最优个体的破坏，采取保留最优个体的方法。将每一代产生的最优个体放在该种群的最后，再继续进行下一代的操作。整个算法的流程图如图１所示。具体实现的遗传操作的主要代码如下： g=300;%进化的代数 bsj=0; for kg=1：1：g   time(kg)=kg;       %*******step 1：计算误差****************        for i=1：1：size         cansu1=kpar(i，：);         selectcode=cansu1;         error=computeitae(selectcode);%计算均方误差;         bsj1=error;         bsji1(i)=bsj1;     end        [oderji，indexji]=sort(bsji1);    bestj(kg)=oderji(1);    bj=bestj(kg);     ji=bsji1+1e-10;%避免除零        fi=1./ji;% 求适应度的值   

  [oderfi，indexfi]=sort(fi)%对适应度值由小到大排列     bestfi=oderfi(size);     bests=kpar(indexfi(size)，：)%保存最大适应度值对应的染色体(参数)         %*******step2：选择和复制************ 图１ 算法流程图 fi_sum=sum(fi);     fi_size=(oderfi/fi_sum)*size;     fi_s=floor(fi_size);     r=size-sum(fi_s);     rest=fi_size-fi_s;     [restvalue，index]=sort(rest);        for i=size：-1：size-r+1         fi_s(index(i))=fi_s(index(i))+1;     end        k=1;     for i=size：-1：1         for j=1：1：fi_s(i)             tempe(k，：)=kpar(indexfi(i)，：);             k=k+1;         end     end         % step 3交叉率不能太大        pc=0.7;     for i=1：2：(size-1)         temp=rand;         if pc>temp             alfa=rand; tempe(i，：)=alfa*kpar(i+1，：)+(1-alfa)*kpar(i，：); tempe(i+1，：)=alfa*kpar(i，：)+(1-alfa)*kpar(i+1，：);         end     end     tempe(size，：)=bests;     kpar=tempe;        %*******step 4：变异*******变异率不能太大     pm=0.15+[1：1：size]*(0.01)/size;     pm_rand=rand(size，codel);     mean=(maxx+minx)/2;     dif=(maxx-minx)/2;        for i=1：1：size         for j=1：1：codel             if pm(i)>pm_rand(i，j)                tempe(i，j)=mean(j)+dif(j)*(rand- 0.4);             end         end     end     tempe(size，：)=bests;%保留最优个体     kpar=tempe;     end bests best_j=bestj(g) figure(1); plot(time，bestj); xlabel('time(s)');ylabel('best j');

3  实验结果

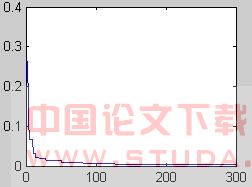
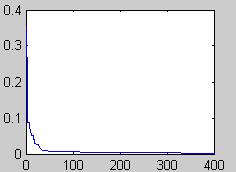
    经过300代进化后，均方误差可以达到0.0029，如图2所示；经过400代之后，均方误差为0.0027，变化曲线如图3所示。图中：横坐标是进化代数，纵坐标是均方误差。     从上面的实验可以看出，参数范围都在最小二乘法估计的参数附近，从进化曲线可以看出，本算法收敛的速度是比较快的，在进化约120代时，就接近了收敛值，同时由于应用了随着进化代数的增加改变变异率的方法，在进化后期，均方误差值略有降低，克服了过早收敛的现象。可以根据精度的要求，运行数次后，得到优化的参考结论参数值。 图2  进化300代的变化曲线 图3 进化400代的变化曲线

4  结论

    从仿真实验可以看出：用简单的最小二乘法粗略估计参数的范围是有效的，在粗略估计范围后，用遗传算法对结论参数进行优化，可以一次优化多个参数，具有简单易行的特点，在所选范围不是太窄的情况下，可以达到较高的精度，而且本算法对范围的大致确定要求不是很严格，具有较好的鲁棒性。

参考文献

[1] 楼顺天等. 基于matlab的系统分析与设计.  [m] . 西安：西安电子科技大学出版社，2001 [2] 刘金琨. 先进pid控制matlab仿真(第2版) .  [m] . 北京：电子工业出版社，2004 [3] loo hay lee， ying li fan. an adaptive real-coded genetic algorithm. applied artifical intelligence. [j]. 2002，16： 457-486 [4] 周林娜，张庆灵，杨春雨.t-s模糊系统的鲁棒局部稳定.系统工程与电子技术.[j]. 2006，28(12) ： 1863-1866